Техническая термодинамика: Учебное пособие (Главы 1-7: Техническая термодинамика. Основные понятия и определения. Смеси идеальных газов), страница 8

Резюме. Показано, что Q и L  обладают общими свойствами, поскольку являются мерами различных форм обмена энергией.

2.5. Первый закон термодинамики для закрытых и

      открытых систем

Закон сохранения  энергии для термодинамических систем:

dq = dU + d l

dq = dU + pdu

TdS = dU + pdu(2.7)

dU = TdS - pdu - Основное термодинамическое тождество

du = TdS - pdu.

Для открытой термодинамической системы характерен обмен веществом. Представим газ, текущий по каналу. Канал выаолнен так, что не препятствует обмену энергиями, но является препятствием для самого газа.

Рис. 2.5.

Продвижение газа по каналу будет сопровождаться D его состояния.

Система между сечениями II и II  II   будет открытой, предположим, что она стационарна.

Элемент газа dm характеризуется только внутренней энергией dU , но и работой, затрачиваемой на его продвижение:  dL = pdW, где dW - объем элемента dm. Или в относительных единицах:

d l = P dW dm = pdu.

Для одного и того же элемента на границе  I - I  d l < 0, так как совершается над системой, а на границе II  - II - dl > 0 , так как совершается самой системой.

Тогда для изменения состояния элементарного участка открытой системы может быть представлено в виде:

(U₁ + p₁u₁) - ( U₂ + p₂u₂)  или  d (U + pu).

Сумма U + pu = h  является параметром состояния, так как входящие в нее слагаемые сами являются параметрами состояния.

Величина  h  ( H) введена была термодинамике Каммерлинг-Оннесом и названа энтальпией. Энтальпия - (в переводе с греческого означает  “согреваю “ ).

Используя первый закон термодинамики, прибавив и вычтя из первой его части  u d p, получим:

dq = dU + pdu = dU + pdu + udp - udp;

так как  pdu + udp= d(pu), то сумма  dU+ d(pu) = d(U + pu) есть полный дифференциал некой функции h. Тогда сучетом этой функции первый закон термодинамики можно переписать:

dq = dh - udp      

(2.8)

dh = TdS  +   udp.

Выражение (2.8) - второй вид уравнения первого закона термодинамики.

Проиллюстрируем это графически.

Рис. 2.6.

udp - площадка, определяющая некоторую элементарную работу l_o, которая в отличие от работы процесса dl = pduназывается располагаемой работой:

dl_о = ±udp ®dq= dh + d l_о                                                                          (2.9)

Из графика, располагаемая работа l_о может быть вычислина следующим образом:  l_о = площадь с 12 в о - площадь оd2в = площадь с 1 о а + 1а2в - площадь о2в = u₁р₁ + 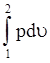-p₂u₂  = u₁р₁ - p₂u₂ + l_о  

 l = l_o  - u₁р₁ +u₂ p₂.

Для элементарного объема из первого закона термодинамики следует:

q = u₂ - u₁ + l_o + u₂ p₂ -  u₁р₁ = (u₂ + u₂ p₂) - (u_{1  +}u₁ р₁ ) + l_o =

h₂ -  h₁ + l_o.

Полученный вывод совпадает с введенным ранее формальным понятием энтальпии ( 2.9).

Гельмгольц ввел в термодинамическую функцию F,  названную им свободной энергией:

dU = dq - pdu ;  dq = TdS.

Прибавим и вычтем  SdT:

dU - TdS - SdT = - pdu - SdT ; TdS - SdT = d(TS);

dU - d(TS) = d( U - TS); d( U - TS) = dF = - pdu - SdT;

F = U - TS.

Первый закон термодинамики относительно свободной энергии:

dF = - pdu - SdT.

Гоббсом было предложено для тепловых расчетов использовать изобарно-изотермический потенциал G.

Получается эта функция состояния из определения ( уравнения ) энтальпии:

dh = TdS + udp; dh - TdS - SdT = udp - SdT;

dh - TdS - SdT =d ( h - TS) = dS; G = h - TS;

dG =  udp - SdT - первый закон термодинамики относительно G.

Анализ уравнений первого закона термодинамики относительно U = f₁(S; u); H = f₂( S;P); F = f₃ (T; u); G = f₄( T;P)показывает, что U, H,  F и G  являются функциями состояния системы и может быть вычислены через параметры состояния. Эти зависимости получили  название характеристических функций.

3. Второй закон термодинамики

3.1. Сущность второго закона термодинамики

Второй закон термодинамики определяет направление протекания термодинамических процессов .