Техническая термодинамика: Учебное пособие (Главы 1-7: Техническая термодинамика. Основные понятия и определения. Смеси идеальных газов), страница 17

^T₁

 

             ^T₂

q =   ( T₂ - T₁ ).

              T₁

 T₂                                    T₂  

cdT =        ( T₂ - T₁ ).

T₁                       T₁

 

            T₂                                                                 T₂

          = 1/ ( T₂ - T₁ )  cdT ®С = f(T).

       T₁                                       T₁

 

                                                                  T₂

Поскольку C = f(T), то решить   cdT  возможно, если известна

                                                                T₁                                                                             

зависимость  C = f(T). Такие зависимости для разных газов, в зависимости от их химической структуры различны. Для упрощения вычислений составлены справочные таблицы. При этом табличные теплоемкости классифицируются по следующим признакам:

- по количеству газа, к которому они относятся:

           t₂                        t₂                        t₁

 _m    =(  _m   t₂   -  _m t₁) / ( t₂ - t₁ );

            t₁                               o                  o

- по роду термодинамического процесса: u = const; p = const:

          t₂                                           t₂                          t₁

_р    = q_p / (t₂ - t₁)  =( _р   t₂   -  _р  t₁) / ( t₂ - t₁ );

         t₁                                                                o                   o

- по интервалу температур:

t₂                                        t₂                         t₁

_u   = q_u /(t₂-t₁)  =(_u   t₂   -  _u    t₁) / ( t₂ - t₁ ).

          t₁                                     o                     o

6.3. Теплоемкость идеального газа при u = const и p = const

            

Как было показано ранее (5.20):

C_p > C_u    и   C_p  - C_u  > 0.

C_p  - C_u = Т (p / T)_u   (u / T)_p  =T(R  R)/( u  p) = R

²²                              RT

                             R/u              R/p

C_p - C_u  = R                                                                        (6.7)

В термодинамике и ее приложениях широко используются следующие соотноешния:

C_p - C_u  =  8314/М ;

C_p ^¢ - C_u  ^¢ =    rR;

k = C_p / C_u  = MC_p / MC_u = C_p ^¢ / C_u  ^¢ .

Для расчетов можно приближенно принять для:

-  одноатомных газов k » 1,67;

-  двухатомных k » 1,4;

- трехатомных k = 1,29.

Значение k может быть определены экспериментально® заманчиво через k определить значения С_р и С_u.

С_р - С_u = R   и  k = С_р / С_u;  С_р = kC_u.

kC_u - С_u = R; С_u( k - 1) = R; k = 1+(R/C_u); C_u = R/(k-1);

С_р = kC_u; С_р = kR/(k-1);

С_u ^¢ = r_о R/ (k-1);  С_p ^¢ = r_о Rk / (k-1).

Вывод: зная k, можно рассчитать значения соответствующих теплоемкостей.

6.4. Основы кинетической теории теплоемкости

Кинетическая теория газа показывает, что давление (р)  идеального газа на стенки сосуда может быть определено соотношением:

P = 2/3N (mW²/2),                                                            (6.8)             где N -  число молекул в 1 м³ объема;  m  - масса молекулы; W - средняя квадратичная скорость поступательного движения молекул:

W = ,         

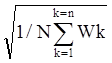
где Wk - скорость поступательного движения любой k-ой молекуле в газе данного состояния.

Умножим левую и правую части ( 6.8) на объем газа V:

PV = 2/3NV (mW²)/2 = 2/3N¹ (mW²)/2,

где N¹ = nV - число молекул газа в V. Для 1 моля:

Pv_m = 2/3nNV_m (mW²)/2 = 2/3N_m (mW²)/2.

Молярная внутренняя энергия газа равна кинетической энергии его молекул: заключенных в V_m: U = N_м (mW² / 2) ®  pV_m = 2 /3 U ®   U = 3 / 2 pV_м  ,так как pV_м = MRT, то U = 2/3 MRT поскольку MR = 8314,4  то U » 12,48 Т; dU / dT = 12,48^*.

В соответствии со сказанным ранее dU = MC_u d¹T® dU / dT =MC_u^**. Сопоставляя (*) и (**), можно записать:

MC_u  = 12,48 кДж/кмоль  К                                           (6.9)

Полученное выражение хорошо согласуется с найденными экспериментально значениями теплоемкостей для одноатомных газов. Это естествено, так как модель идеального газа наиболее полно соответсвует одноатомным газам.