Если представить себе формулы разных видов работ: механической при кручении: dLм = Mк dj; при прямолинейном движении: dLперем= Fdl, F= рS ,где Мк - крутящий момент; dj - угол поворота; F= рS – сила; р- давление; S – площадь; dl – перемещение;
электрической dLэл = Еэлde, где Еэл - напряженность электрического поля; de - заряд; магнитной dLмаг = НмагdМм, где Hмаг - напряженность магнитного поля; Ммаг - магнитный момент.
Очевидно, что в любом случае для определения работы необходимо знание двух величин, однозначно ее определяющих: величины, выполняющей роль движущего фактора ( p, Mк, Еэл, Нмаг ... ), и величины, по которой можно судить о наличии самого процесса : j, l , e, Mмаг ....
При этом первый фактор будет определять направление и интенсивность процесса, а второй - положение системы.
В механике величины первого вида получили значение обобщенных сил Хi , второе - обобщенных координат dxi:
dLi = X1dxi.
В физике (в силу исторических причин) величины, характеризующие движущие силы процесса называются потенциальными P. Причем потенциал некоторого силового поля равен равнодействующей силе, действующей в этом поле, взятой с обратным знаком: X1 = - P1.
В термодинамике потенциалами взаимодействия любого рода называют физические величины, различие значений которых в термодинамической системе и окружающей среде является причиной возникновения взаимодействия данного рода.
Координатами термодинамического состояния называются физические величины, характеризующие наличие взаимодействия того или иного рода.
То есть координата обязательно меняется только, если существует определенное взаимодействие. Если такового нет, то и координата остается неизменной.
Количество взаимодействий всегда пропорционально сумме соответствующей координате и совпадает с ним по знаку.
Потенциалы - факторы интенсивные; координаты - экстенсивные, так как при разделении системы на части P каждой из них остается const, а координаты D пропорционально размеру каждой части и количеству вещества в ней. Но в однородной системе удельные экстенсивные факторы приобретают свойства интенсивных.
Рассмотрим более подробно тепловые процессы. Очевидно, что движущей силой таких процессов является разность температур. Интенсивность процесса растет при увеличении разности температур. Следовательно потенциалом является температура.
Поиск такой величины велся длительное время и только в 1854 году Клаузиус нашел способ определения такой величины, названной им в 1862 году энтропией S:
dQ = TdS . (2.6)
Сложность поиска S заключается в том, что соответсвующая физическая величина не оказывает непосредственного макроскопического воздействия на приборы или органы чувств человека. Размерность энтропии
[ S] = Дж/К; удельной [ S] = Дж/кг К.
Физический смысл энтропии -это мера хаотичности беспорядочного теплового движения.
Повышение S соответствует понижению упорядоченности в расположении микрочастиц и в распределении энергии между ними.
Количественная связь S и микроскопических характеристик устанавливается методами статистической термодинамики.
Запишем уравнение (2.6) в относительных величинах:
dq = TdS.
При подводе теплоты к системе: dq > 0 ® dS > 0; при отводе теплоты dq < 0 ® dS < 0.
Уравнение состояния теплового процесса записывается в видеT = T(S).
Рис. 2.4.
Графическое изображение этого уравнения называется энтропийной ST - диаграммой.
Площадь под кривой 1-2 сдедовательно теплота процесса Q:
Q
= ![]() =
= 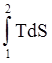 .
.
Энтропийная
диаграмма часто называется тепловой диаграммой. Переход системы из состояния 1
в состояние 2 может быть осуществлена разными путями. Следовательно Q -
не может быть полным дифференциалом, и интеграл по замкнутому контуру равен
нулю![]() ¹ 0.
¹ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.