Техническая термодинамика: Учебное пособие (Главы 1-7: Техническая термодинамика. Основные понятия и определения. Смеси идеальных газов), страница 6

В термодинамике обычно не возникает необходимости использовать потенциальную энергию.

Предполагается, что кинетическая энергия системы либо равна нулю, либо пренебрежимо мало отличается от него. Следовательно, под энергией системы понимают ее внутреннюю энерги: DЕ = DU , для тер-модинамической системы.

В термодинамике и ее приложениях обычно бывает достаточно знать изменения внутренней энергии системы. То есть за нулевое значение может быть принято любое значение и в любом состоянии системы.

Чтобы судить об абсолютной величине U , необходимо обратиться к микроструктуре вещества и учесть строение, структуру его, строение молекул, атомов и так далее.

Согласно теории относительности: Е = mс².

2. Первый закон термодинамики

2.1. Сущность первого закона

Закон сохранения энергии в общем виде можно записать:

DЕ = DU = å L ⁱ _k  + Q.

k=1

Механическая работа в термодинамических процессах считается положительной, когда деформация системы происходит с уменьшением внутренней энергии, то есть  когда система совершает работу  над окружающей средой.

Такое же правило законов применяют и для других видов работ, в связи с чем знаки количеств нетермических воздействий всегда противоположны знакам количеств соответствующих работ.

В дифференциальном виде можно записать:

dQ = dU + ådL ⁱ_k .

k           

В  дальнейшем будим принимать во внимание только работу, совершенную термодинамической системой ® Lⁱ ® L.

dQ = dU + ådL_k.                                                         (2.1)

k           

Уравнение ( 2.1) представляет собой запись первого закона термодинамики. Физический смысл первого заrона термодинамики заключается в том, что теплота подведенная к системе частично возвращается в окружающую среду в виде различных видов работ, частично расходуется на изменение внутренней энергии системы.

Как было отмечено ранее, в термодинамике рассматриваются, как правило, простые термодеформационные системы. Следовательно к рассмотрению принимается только механическая работа деформации системы.

Тогда   первый закон термодинамики можно записать в таком виде:

dQ = dU + dL

 Q = DU + L                                                                       (2.2)

Q_1-2 = U₂  - U₁ + L_1-2

Или в удельных величинах ( отнесенных к массе):

dq = dU + dl

q_{1- 2} =U₂ - U₁+ l_1-2                                                                                              (2.3)

2.2 . Работа

Чтобы отпределить работу деформации замкнутой системы, следует рассмотреть бесконечно малое изменение объема, занимаемого рабочим телом.  В термодинамике в качестве рабочих тел принимаются ( чаще всего) легкодеформируемые: пар, газ.

Рис. 2.1.

Газ, находящийся в оболочке, способен деформироваться и имеет давление Р₁ равномерно распределенное по контрольной поверхности и уравновешенное наружным давлением Р. При бесконечно малом DР,контрольная поверхность ( КП) переместиться в сторону окружающей Среды на бесконечно малое расстояние dx, которое на разных участках контрольной поверхности может быть разным. Тогда работа на элементарном участке df будет:

dL = pdfdx dV

dL = pdV ® L_1-2 =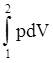                                            (2.4)

dl = pdu.

Рис.2.2.

В общем случае зависимость p от  uможет быть любой. Следовательно работа термодинамического процесса 1-2 будет равна площади под кривой 12. Если зависимость другая, то и площадь будет 1 1 n 2 < 12, то есть L зависит от пути перехода системы из состояния 1 в состояние 2. А работа по замкнутому контуру не равна 0 , а L_ф= площадь внутри цикла 12 n. Следовательно нельзя писать dL , а  надо dL = L_1-2. Следовательно L характеристика не системы, а совершаемого ею процесса.

В относительных величинах:

dq =du +dl = du + pdu

dq =du + pdu(2.5)

 

2.3.  Потенциалы термодинамической системы.

        Энтропия