Техническая термодинамика: Учебное пособие (Главы 1-7: Техническая термодинамика. Основные понятия и определения. Смеси идеальных газов), страница 18

Молекула одноатомного газа имеет три степени свободы. На каждую степень свободы расходуется MC_u /3 = 4,16 кДж/кмоль К . Двухатомные газы имеют пять степеней свободы ( 3 поступательных + 2 вращения ).

Если предположить, что на каждую степень свободы приходится то же колличество энергии = 4,16, то MC_u = 5   4,16 = 20,8.

Для трехатомного MC_u = 6  4,16 = 24,96.

Экспериментальные значения С для соответсвующих газов качественно подтверждают значения молярных теплоемкостей, найденных расчетным путем. Расхождение между ними видетельствует о том, что кинетическая теория не учитывает внутримолекулярного движения атомов и сил взаимодействия между молекулами. Эти факторы могут быть учтены квантовой теорией:

d₂

MC_u = d₁(MR/2) + MR ((/T)²e^/T)/( e ^/T-1)²,

                                1

где d₁ - часть степени свободы поступательного и вращательного движения молекулы; d₂ - часть степени свободы внутримолекулярных колебаний; - характеристическая температура  q  = fn, где n - частота колебаний; T - температура газа; e - основание натурального логарифма.

7. Смеси идеальных газов

7.1. Закон Дальтона

В теплотехнических установках в качестве РТ часто используются  не однородные газы, а их смеси (атмосферный возду).

Если в смеси нет химических реакцией, то она подчиняется основным газовым законам т уравнениям состояния.

Каждый газ, входящий в газовую смесь, оказывает на стенки сосуда давление, величина которого не зависит от присутствия в этом объеме других газов. Такое давление называется парциальным.

Дальтон установил, что при постоянной температуре полное давление смеси нескольких газов, химически не реагирующих между собой, равно сумме их парциальных давлений:

P_m = 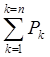                                                                       (7.1)

n - количество газов, входящих в смесь.

Количество отдельных газов в смеси может быть задано массовыми g_k   объемными r_k  долями. Если смесь газов состоит из n отдельных газов, то:

g_k  = m_k /  m_k  = m_k / m_m,

где m_k - масса k - го газа в смеси; m_m - масса смеси газов:

 g_k =  1 или 100 %.

Если смесь задана объемными долями, то:

r_k  = V_k / V_m, где V_k  - парциальный объем k-гогаза, входящего в состав смеси. V_m - молярный объем смеси.

r_k = V_k / V_m =( n_k (Mu)_k),

где n_k - количество вещества k-го газа а смеси, моль; (Mu)_k - молярный объем k-го газа в смеси.

В соответствии с законом Авагадро: все газы при одинаковых условиях содержат в равных объемах равное число молекул ®(Mu)_k =const ® r_k = n_k / n_m  ®  r_k = 1 или 100 %.

Вывод: объемные и молярные доли численно равны между собой:

r_k = g_k.

7.2. Уравнение состояния смеси идеальных газов

Для k-го газа, находящегося в газовой смеси уравнение состояния может быть записано в виде:

p_k u_k = R_kT_m                                                                      (7.2)

Для молярного объема уравнение состояния будет иметь вид:

p_kV_Mk = R_kM_kT_m ® R_k = 8314,4/M_k ®

Уравнение состояния  Клайперона-Менделеева:

 p_kV_k = 8314 T_m                                                             (7.3)

Для смеси газов можно записать:

p₁V_m = m₁R₁T_m;

p₂V_m = m₂R₂T_m;

.........................;

..........................;

p_nV_m = m_nR_nT_m

 V_mp_k = (m₁R₁ + m₂R₂ + ... + m_nR_n)*T_m

 _{из уравнения}            обозначим m_mR_m

_{Дальтона}

²

 p_m

Уравнение смеси газов:

p_mV_m =  m_mR_mT_m                                                          (7.4)

Разделив все члены выражения (*) на m_m, получим выражения для расчета удельной газовой постоянной смеси (m_k / m_m = g_k):

R_m = g_kR_k  , R_kM_k = 8314,4                                   (7.5)

R_m = 8314 ( g_k / M_k)                                          (7.6)

Вывод: Для определения удельной газовой постоянной не нужно знать R_k  для каждого газа. Достаточно знать лишь массовый состав газа g_k  и мольные доли компонентов газовой смеси.