Уравнивание нивелирных сетей (Глава 2 дипломного проекта), страница 8

                                                           (106)

Пользуясь относительной малостью , разложим выражение (106) в ряд Тейлора и ограничимся членами первого порядка

                                                               (107)

Здесь обозначено

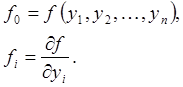                                                                              (108)

Введем вектор частных производных

                                                                                 (109)

и представим линеаризованное выражение функции (107) в матричной форме

                                                                                     (110)

Обратный вес функции может быть вычислен по одной из следующих формул

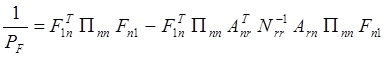                                            (111)

- через элементы обратной матрицы   

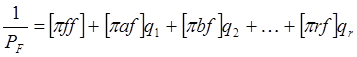                                                 (112)

-  через переходные коэффициенты .

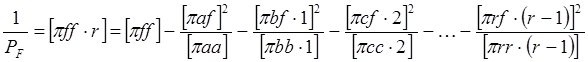          (113)

- в дополнительном столбце схемы решения нормальных уравнений.

Оценка точности функции завершается вычислением ее средней квадратической ошибкой по формуле

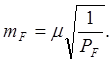                                                                                         (114)

2.2.2. Уравнивание нивелирной сети коррелатным способом

Будем уравнивать нивелирную сеть, представленную на рисунке.

Исходные данные приведены в таблицах 4 и 5.

Число всех измерений n=8, число необходимых измерений t=4, число избыточных измерений r = n-t = 8-4 = 4.

Составим условные уравнения связи

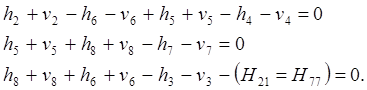
Сложим все известные величины в уравнениях и обозначим , тогда уравнения примут вид

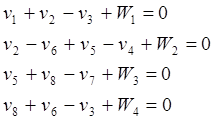
-  условные уравнения поправок.

Вычислим свободные члены

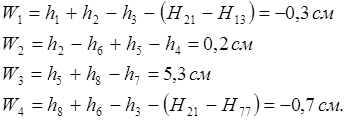
С учетом W_i запишем

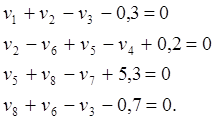
Составим весовую функцию

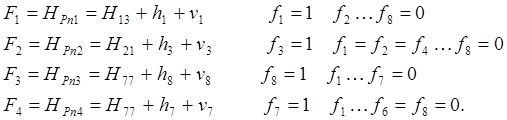
Для удобства дальнейших расчетов составим таблицу 9

                                                                                                  Табл.9

Коэффициенты условных уравнений и функций

№№ П/П	p	a K1	b K2	c K3	d K4	F	S	p	v	pv
1	1,54	1	0	0	0	1	2	0,65	-0,80	-0,52
2	2,04	1	1	0	0	0	2	0,49	0,39	0,19
3	1,00	-1	0	0	-1	0	-2	1,00	-0,71	-0,71
4	1,72	0	-1	0	0	0	-1	0,58	-1,21	-0,70
5	0,78	0	1	1	0	0	2	1,29	-0,76	-0,98
6	2,00	0	-1	0	1	0	0	0,50	1,04	0,52
7	2,08	0	0	-1	0	0	-1	0,48	3,49	1,68
8	2,32	0	0	1	1	0	2	0,43	-1,05	-0,45

å              1          0           1          1           1          4                     =9,45

   

         

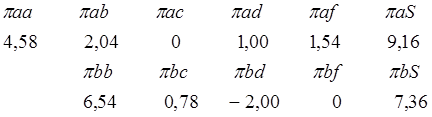
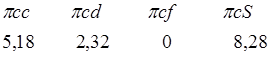
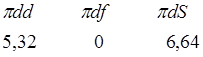
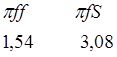
Составим систему нормальных уравнений коррелат

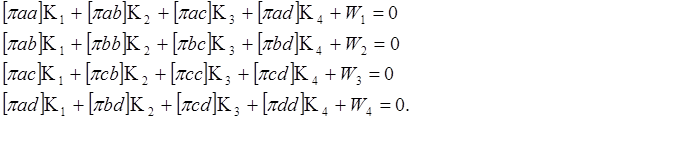
или

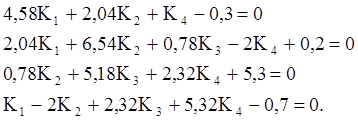
- суммарное уравнение.

Решение нормальных уравнений коррелат выполнено на компьютере по программе ТМОГИ. Исходными данными будут являться матрица коэффициентов параметрических уравнений поправок  А  и веса измерений.

Результаты выдачи с ЭВМ: матрица коэффициентов нормальных уравнений коррелат N

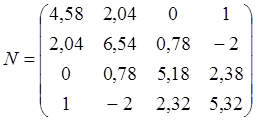
и обратная матрица

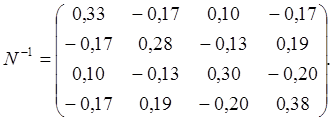
А также мы получим вектор коррелат и вектор поправок

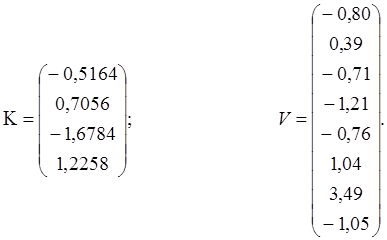
Контроль решения системы нормальных уравнений коррелат

Заключительный контроль уравнительных вычислений

                                                       Табл. 10

Уравненные значения превышений

№№ превышений	Уравненные превышения, h+v
1 2 3 4 5 6 7 8	6.117 8.308 5.578 1.341 4.694 11.661 -0.916 -5.610

Контроль уравнивания

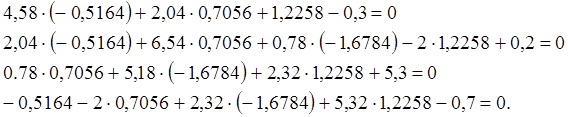
Выполним оценку точности.

Средняя квадратическая погрешность единицы веса

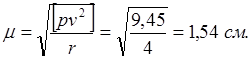
Обратный вес функции F₁

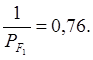
Средняя квадратическая погрешность функции F₁