![]() (34)
(34)
Это выражение представляет собой матричную запись системы t линейных уравнений, именуемых нормальными, из решения которых может быть получен вектор Xt1, то есть вектор поправок к приближенным значениям параметров. 3десь Ntt - матрица коэффициентов нормальных уравнений.
Вt1 - вектор свободных членов нормальных уравнений.
Дальнейший ход уравнительных вычислений можно
представить так. С помощью матричного равенства (28) получаем вектор Vn1
поправок к измеренным величинам, и затем вектор Yn1
уравненных значений измеренных величин ![]()
![]()
Здесь
![]()
Уравненные значения параметров могут быть вычислены с помощью равенств (22). При ручном счете, чаще всего целесообразнее пользоваться уравнениями и2 формулами, записанными в обычной алгебраической форме. Такую запись будем именовать развернутой или поэлементной записью, поскольку операции с матрицами развертываются здесь в обычные алгебраические операции с элементами матриц.
Представим нормальные уравнения (34) в поэлементной записи. Для этого развернем выражение (30)
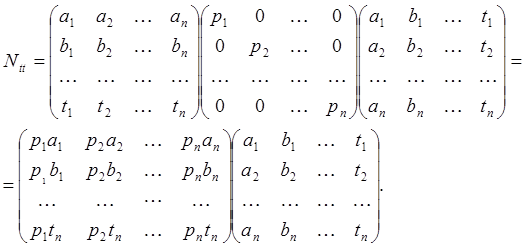
Производя до конца перемножение матриц и используя при этом обозначения Гаусса
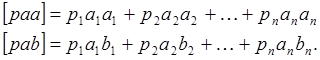 (35)
(35)
и так далее получаем в развернутом виде матрицу коэффициентов нормальных уравнений
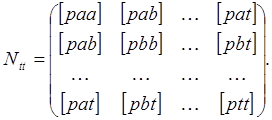 (36)
(36)
Аналогичным образом получаем для вектора свободных членов (31)
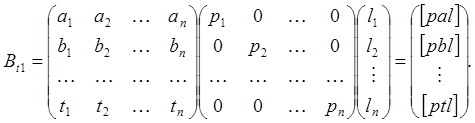 (37)
(37)
Используя выражения (36), (37) и (27), записываем нормальные уравнения (34) в таком виде
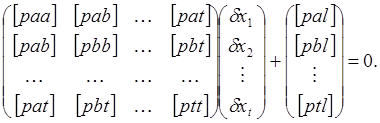 (38)
(38)
Отсюда переходим в поэлементной записи нормальных уравнений (34), для случая уравнивания неравноточных измерений
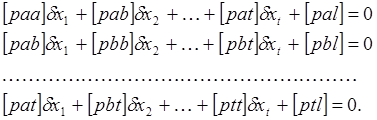 (39)
(39)
Коэффициенты [paa], [pbb], ..., [ptt], расположенные по главной диагонали, именуются квадратичными. Они всегда положительны. Остальные коэффициенты [раb], [рас], ..., [pat] и др. именуются неквадратичными.
Рассмотрим способ Гаусса на примере решения в общем виде системы нормальных уравнений с тремя неизвестными
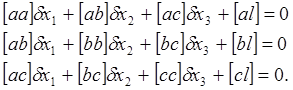 (40)
(40)
Исключим из уравнений (40) неизвестное ![]() . Для этого умножим первое уравнение
первоначально на величину -[ab]/[aa] и сложим со вторым
уравнением, затем на величину - [ac]/[aa] и сложим с третьим
уравнением. В результате получаем
. Для этого умножим первое уравнение
первоначально на величину -[ab]/[aa] и сложим со вторым
уравнением, затем на величину - [ac]/[aa] и сложим с третьим
уравнением. В результате получаем
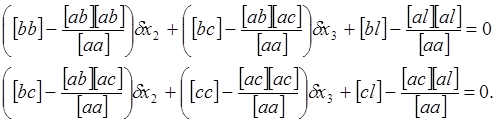 (41)
(41)
Введем обозначения
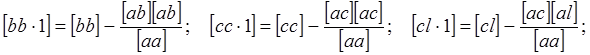
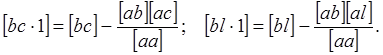 (42)
(42)
С учетом этих обозначений, система (41) примет вид
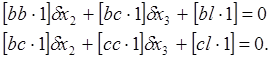 (43)
(43)
Исключим из (43) неизвестное
![]() . Для этого первое уравнение из (43)
умножим на величину
. Для этого первое уравнение из (43)
умножим на величину ![]() сложим со вторым уравнением. В
результате получим
сложим со вторым уравнением. В
результате получим
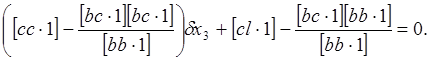 (44)
(44)
Введем обозначения
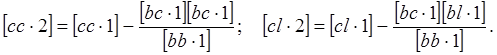 (45)
(45)
Теперь уравнение (44) примет вид
![]() (46)
(46)
Из этого уравнения находим ![]() .
Подставляя
.
Подставляя ![]() в первое уравнение из (43), находим
в первое уравнение из (43), находим ![]() . Наконец, подставляя значения
. Наконец, подставляя значения ![]() и
и ![]() в
первое уравнение из (40) , находим
в
первое уравнение из (40) , находим ![]() .
.
Соберем а одну группу уравнения, из которых непосредственно находят значения неизвестных
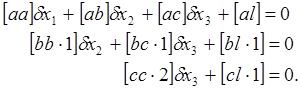 (47)
(47)
Эту группу именуют эквивалентной системой уравнений. Систему (47) часто именуют также системой преобразованных уравнений.
Пользуясь системой (47), представим в явном виде каждое неизвестное
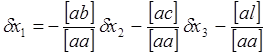
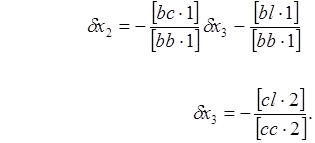 (48)
(48)
Эту группу равенств принято называть системой элиминационных yравнений.
Символы ![]() и т.д. именует
символами Гаусса. Они развертываются по определенному правилу, которое предопределяет
и порядок выполнения операций для получения численного значения символа.
и т.д. именует
символами Гаусса. Они развертываются по определенному правилу, которое предопределяет
и порядок выполнения операций для получения численного значения символа.
Правило развертывания символов Гаусса состоит в следующем. Символ развертывается в разность. Уменьшаемым разности является развертываемый символ, но со значком, уменьшенным на единицу (значок ноль не пишется). Вычитаемым членом является дробное выражение. Его знаменателем является квадратичный коэффициент, буквы которого в алфавитном порядке соответствуют значку развертываемого символа. Числителем дробного выражения является произведение двух символов, каждый из которых получается из уменьшаемого путем последовательной замены одной из его букв буквой знаменателя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.