Уравнивание нивелирных сетей (Глава 2 дипломного проекта), страница 7

В результате получим функцию Лагранжа

                                                (87)

Теперь задача сводится к отысканию абсолютного минимума этой функции. Перепишем выражение (87) в виде

и продифференцируем по вектору . Приравняв вектор частных производных нулевому вектору, получаем

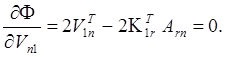                                                                       (88)

Отсюда следует

или, после транспонирования

                                                                                    (89)

Умножим это равенство слева на матрицу обратных весов результатов измерений   Пnn и учтем, что

                                                                             (90)

Тогда получим

                                                                                   (91)

Это формула для вычисления вектора поправок с помощью вектора коррелат. Остается определить вектор коррелат. Подставим выражение для вектора поправок (91) в матричное уравнение (84)

и введем обозначение

                                                                                   (92)

В итоге получим

                                                                                   (93)

Это матричная запись системы уравнений, именуемых нормальными уравнениями коррелат. Из решения матричного уравнения (93) может быть определен вектор коррелат   .

Развернем матричное выражение (91)

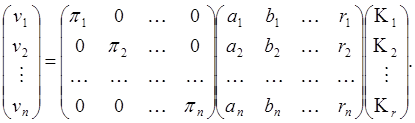
Перемножив матрицы и приравняв соответствующие элементы правой и левой частей матричного равенства, получаем поэлементную запись выражений для поправок (91)

                                      (94)

Развернем матрицу коэффициентов нормальных уравнений коррелат

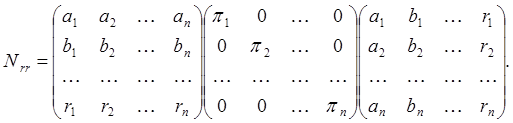
Окончательно, после перемножения матриц, получаем

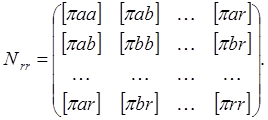                                                               (95)

Заменяя в уравнении (93) буквенные обозначения матриц их выражениями  (95), (86), (83), получаем развернутую запись нормальных уравнений коррелат

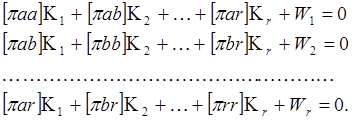                                                 (96)

В отличие от параметрического способа уравнивания, свободные члены нормальных уравнений получаются без каких-либо преобразований путем переноса их из условных уравнений поправок.

Порядок вычисления коэффициентов нормальных уравнений здесь такой же, как и в параметрическом способе, а потому не требует особых пояснений. Заметим лишь, что вместо весов в вычислении коэффициентов здесь участвуют обратные веса результатов измерения   p  .

Рассмотрим способ решения нормальных уравнений методом обращения.

Систему нормальных уравнений

умножим справа на обратную матрицу

Выразим вектор коррелат

                                                                                        (97)

Или

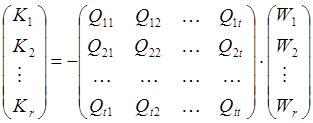                                                        (98)

Отсюда коррелаты могут быть найдены по формулам:

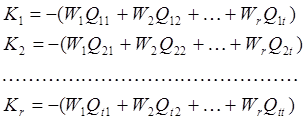                                                         (99)

Складывая нормальные уравнения (96) получаем равенство

                                                (100)

которое служит заключительным контролем вычисления коррелат.

Напишем условие наименьших квадратов

и заменим в нем вектор Vn1 выражением (91). В результате получим

Учитывая, что      пишем

                                                                        (101)

Из выражения (84) следует

Принимая это во внимание, переписываем (101) в виде

                                                                             (102)

Это равенство служит заключительным контролем уравнивания. В поэлементной записи равенство (102) выглядит так

или

                                                                                       (103)

Для вычисления средней квадратической ошибки единицы веса  применяют формулу

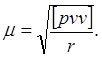                                                                                           (104)

Знаменателем здесь является число условных уравнений

Каждое избыточное измерение приводит к образованию одного математического соотношения типа (76),то есть число условных уравнений равно числу избыточных измерений.

Затем рассмотрим задачу оценки точности функции уравненных величин

                                                                               (105)

Для ее решения произведем предварительно линеаризацию функции, подставив в нее вместо  значения (75)