Уравнивание нивелирных сетей (Глава 2 дипломного проекта), страница 5

2) Вычислены истинные ошибки результатов измерений  по формуле

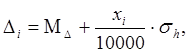
где - математическое  ожидание  случайной  ошибки  ,

-среднее  квадратическое  отклонение  измеренного  превышения,

x_i взяли из таблиц нормально распределенных случайных чисел /5/:    

1,393   -1,783   -0,105   -1,339   1,041   0,279   -1,805   -1,186

3) Вычислены измеренные значения превышений

4) Вычислены  веса  результатов  измерений

где  с = 7,2,

Li,км – длина хода.

Результаты моделирования  приведены в таблице 3:

Табл. 3

Моделирование нивелирной  сети

№№ пп	, см	hизм, м	Pi
1 2 3 4 5 6 7 8	1,4 -1,8 -0,1 -1,3 1,0 0,3 -1,8 -1,2	6,125 8,304 5,585 1,353 4,702 11,651 -0,951 -5,600	0,65 0,49 1,00 0,58 1,29 0,50 0,48 0,43

5) Средняя квадратическая ошибка единицы веса вычислена по формуле Гаусса

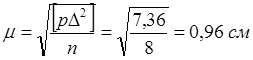, где   n – число измерений.

2.1.3. Уравнивание нивелирной сети  параметрическим  способом

Будем уравнивать нивелирную сеть, представленную на рисунке. Измеренные превышения и их веса представлены в таблице 4, отметки исходных пунктов в таблице 5.

                                              Табл.4

                                  Результаты измерений

№ №	Измеренные превышения  h, м	Длины ходов L, км	Веса превышений  pi
1 2 3 4 5 6 7 8	6,125 8,304 5,585 1,353 4,702 11,651 -0,951 -5,600	11,1 14,8 7,2 12,4 5,6 14,3 15,1 16,8	0,65 0,49 1,00 0,58 1,29 0,50 0,48 0,43

                             Табл. 5

                               Исходные отметки

№ марок	Отметки, м
М.13 М.21 М.77	183,506 192,353 191,880

Число всех измерений n=8, число необходимых измерений t=4. Параметры x₁, x₂, x₃, x₄ – отметки определяемых пунктов.

Составим параметрические уравнения связи

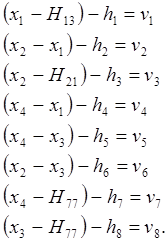
Приближенные значения параметров

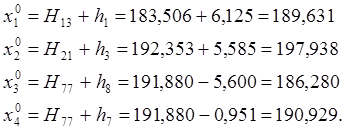
Составим параметрические уравнения поправок

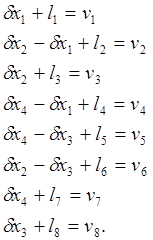
С учетом параметрических уравнений связи и приближенных значений параметров найдем значение свободных членов параметрических уравнений поправок l_i:

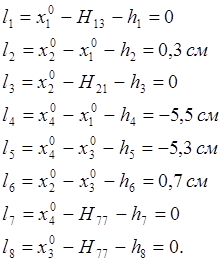
С учетом свободных членов параметрические уравнения поправок запишем в следующем виде

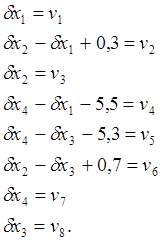
Запишем весовую функцию

Все дальнейшие вычисления поместим в таблицу 6.

                                                                                                          Табл. 6

Таблица параметрических уравнений

№№ уравнений	p	а	b	c	d	l,см	S		v	pv
1	0,65	1	0	0	0	0,0	1,0	0,90	-0,80	-0,52
2	0,49	-1	1	0	0	0,3	0,3	0,68	0,39	0,19
3	1,00	0	1	0	0	0,0	1,0	1,39	-0,71	-0,71
4	0,58	-1	0	0	1	-5,5	-5,5	0,81	-1,21	-0,70
5	1,29	0	0	-1	1	-5,3	-5,3	1,78	-0,76	-0,98
6	0,50	0	1	-1	0	0,7	0,7	0,70	1,04	0,52
7	0,48	0	0	0	1	0,0	1,0	0,66	3,49	1,68
8	0,43	0	0	1	0	0,0	1,0	0,60	-1,05	-0,45

å -1         -3         -1         3       -9,8      -5,8                                 

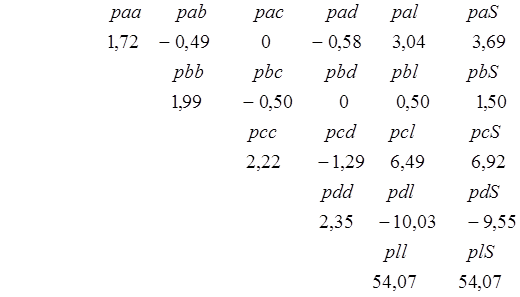
Составим систему нормальных уравнений

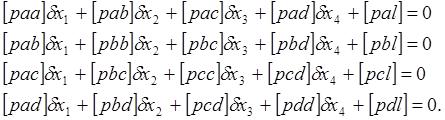
С учетом коэффициентов перепишем систему нормальных уравнений:

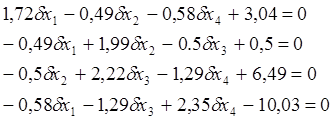
     -  суммарное  нормальное уравнение.

Решение нормальных уравнений выполним на компьютере по программе ТМОГИ. Исходными данными будут являться матрица коэффициентов параметрических уравнений поправок Аnt и вектор свободных членов L_n1, а также веса результатов измерений  p_i.