Уравнивание нивелирных сетей (Глава 2 дипломного проекта), страница 4

представляем линейное выражение (56) в матричной форме

                                                                                    (58)

Заменим в формуле 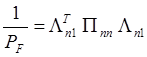           его выражением

            (/3/,страницы  71,73)

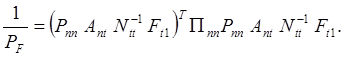                                                   (59)

Произведя транспонирование выражения в скобках и приняв во внимание, что

                                                                             (60)

получаем

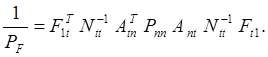
Далее, принимая во внимание, что        и          

переходим к равенству

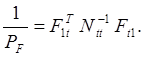                                                                                              (61)

Полученная формула позволяет вычислить обратный вес функции с помощью обратной матрицы коэффициентов нормальных уравнений и вектора коэффициентов линеаризованной функции. Развернем матрицы в этом выражении

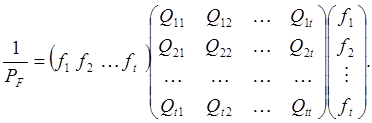                                              (62)

Перемножая матрицы и учитывая симметричность , получаем в поэлементной записи формулу для вычисления обратного веса функции (52) с помощью весовых коэффициентов

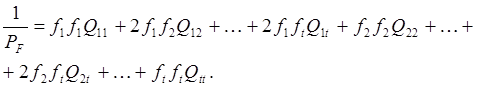                             (63)

Формулу (61) с учетом обозначения    можно представить в следующем виде

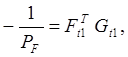                                                                                       (64)

или в поэлементной записи

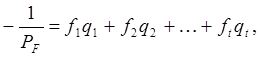                                                               (65)

где  q- переходные  коэффициенты.

Для вычисления [pvv]  получены  формулы

и

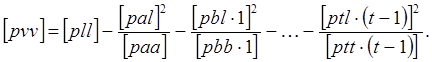
Приравнивая правые части этих выражений, получаем

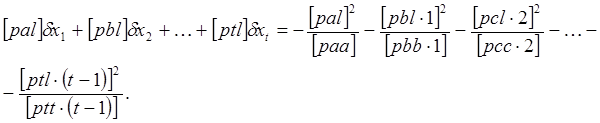        (66)

Это равенство, записанное применительно к системе (39), справедливо и для любой другой системы нормальных уравнений. Применим его к системе переходных нормальных уравнений.

Заменим  

В результате, по аналогии с (66), приходим к равенству

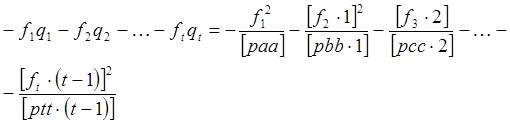
или, принимая во внимание (65),

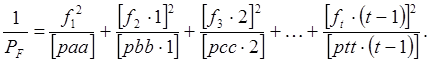                                    (67)

Полученная формула позволяет вычислить вес функции попутно с решением нормальных уравнений по алгоритму Гаусса.

Для оценки точности уравненного параметра  будем рассматривать простейшую линейную функцию, содержащую в качестве аргумента собственно параметр с коэффициентом, равным единице. Очевидно, вес такой функции и будет являться весом искомого параметра.

Для оценки точности  x₁, такая функция будет иметь вид

                                                                                 (68)

Здесь   

Для  оценки  точности  x₂

                                                                                (69)

Здесь    

Для оценки точности    x_t

                                                                                 (70)

Здесь     

Применяя к функциям (68) - (70) формулу (63) получаем

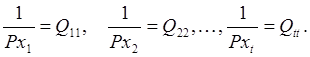                                                        (71)

Среднюю квадратическую ошибку результата измерения по результатам  уравнивания   вычисляют по формуле

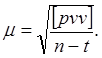                                                                                           (72)

Оценку точности функций уравненных аргументов и самих аргументов завершают вычислением их средних квадратических погрешностей. Это делается по формулам

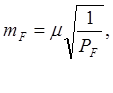                                                                                         (73)

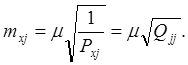                                                                             (74)

Здесь m - средняя каадратическая погрешность единицы веса, вычисляемая по формуле (72)

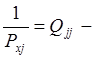обратные веса искомых параметров равны диагональным элементам обратной матрицы .

2.1.2. Моделирование нивелирной сети

Схема нивелирной сети на рисунке взята из работы /4/. Отметки марок приведены в таблице 1, а длины ходов и уравненные значения превышений в таблице 2.

Схема нивелирной  сети

                                               Табл. 1

Отметки  исходных  пунктов

№ марок	Отметки, м
М.13 М.21 М.77	183,506 192,353 191,880

                                             Табл. 2

Уравненные превышения

№№	Длина хода L, км	Превышения  , м
1 2 3 4 5 6 7 8	11,1 14,8 7,2 12,4 5,6 14,3 15,1 16,8	6,111 8,322 5,586 1,366 4,692 11,648 -0,933 -5,588

Моделирование результатов измерений  выполнено в следующей  последовательности:

1) Уравненные превышения приняты за истинные