Уравнивание нивелирных сетей (Глава 2 дипломного проекта), страница 6

В итоге получим матрицу N коэффициентов нормальных уравнений и обратную матрицу .

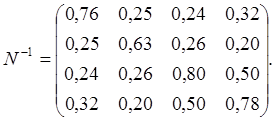
Вектор свободных членов

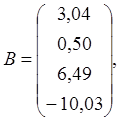
а также поправки к параметрам и вектор поправок к измерениям

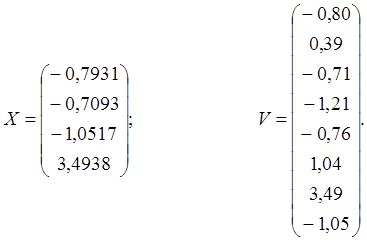
Контроль решения системы нормальных уравнений

Выполним заключительный контроль уравнивания

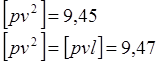
Контроль уравнивания.

                                                                                                      Табл. 7

Уравненные значения превышений

№№ превышений	Уравненные превышения	Функции параметров

                                                                   Табл. 8

                     Уравненные отметки узловых пунктов

№№ узлов	x, м
1 2 3 4	189,623 197,931 186,269 190,964

Затем выполним оценку точности.

Средняя квадратическая ошибка единицы веса

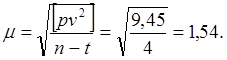
Средняя квадратическая ошибка измеренного превышения на 1 км хода

Обратный вес функции    

Средняя квадратическая погрешность уравненных величин

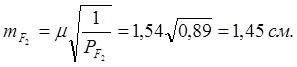
Обратные веса параметров и их средние квадратические ошибки

2.2. Коррелатный способ

2.2.1. Общие сведения

В отличие от параметрического способа уравнивания, где на основе принципа наименьших квадратов решались уравнения, связывающие уравненные значения измеренных величин с системой искомых параметров, в коррелатном способе на основе принципа наименьших квадратов решают, так называемые, условные уравнения связи, которым должны удовлетворять истинные, а также уравненные значения измеряемых величин. Эти уравнения составляются на основе математических свойств геодезических сетей.

Рассмотрим задачу коррелатного уравнивания. Пусть выполнено n   измерений, результаты которых  имеют, соответственно, веса . Полагаем, что уравненные значения измеренных величин , вычисляемые как суммы измеренных значений и искомых поправок

                                                                   (75)

должны удовлетворять следующей системе независимых условных уравнений связи

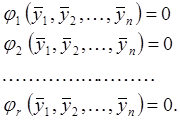                                                                              (76)

Число таких уравнений      всегда меньше числа измерений, то есть       

Если подставить в уравнения (76) результаты измерений, то в силу наличия в этих результатах неизбежных ошибок уравнения не будут удовлетворяться и в правой части получатся невязки   

                                                    (77)

Задача коррелатного уравнивания состоит в том, чтобы определить такие поправки v_i к измеренным величинам, которые привели бы измеренные величины в соответствие с условными уравнениями связи, и, кроме того, удовлетворяли бы принципу наименьших квадратов.                      

                                                                                           (78)

Подставим в уравнения (76) вместо y_i  их значения (75)

                                  (79)

Пользуясь относительной малостью поправок v_i, разложим эти выражения в ряд Тейлора и ограничимся членами первого порядка

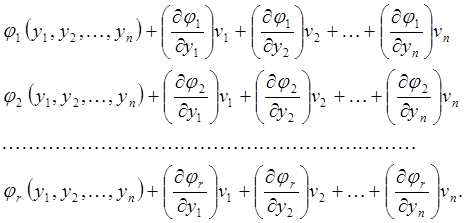                               (80)

Введя обозначения

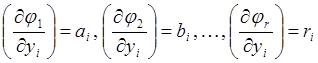                                                       (81)

и принимая во внимание (77), переписываем уравнения (80) в таком виде

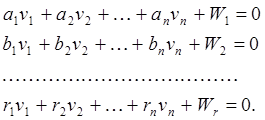                                                                (82)

Полученные уравнения, которые суть линеаризованные условные уравнения связи, принято называть условными уравнениями поправок. Коэффициентами в них являются частные производные функций, представляющих условные уравнения, по измеренным величинам, а свободными членами - невязки условных уравнений связи, получаемые при подстановке результатов измерений.

Введем матрицы

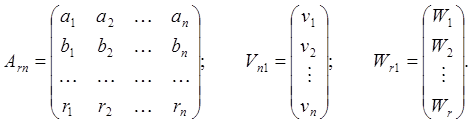                             (83)

Тогда система условных уравнений поправок (82) запишется в виде одного матричного уравнения

                                                                                    (84)

Из экстремального равенства метода наименьших квадратов, которое запишем в матричной форме

                                                                                    (85)

вычтем левую часть матричного уравнения (84), умноженную на вектор множителей ,  именуемых коррелатами

                                                                             (86)