Символам дробного выражения присваиваются значки уменьшаемого.
Примеры развертывания символов Гаусса:
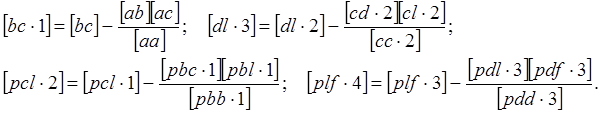
Развертывание символов со значками, большими
единицы, может быть продолжено. Продолжим развертывание символа ![]() .
.
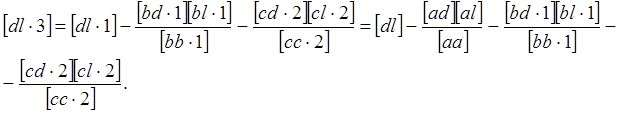
При ручном счете целесообразно производить текущий контроль вычисления неизвестных. Заключается он в том, что неизвестные в порядке их получения из элиминационных уравнений (48), тотчас же подставляются в соответствующие преобразованные уравнения (47), которые при правильном счете должны удовлетворяться.
Более простым является контроль подстановкой неизвестных в так называемое, суммарное уравнение, которое получают суммированием всех нормальных уравнений (39).
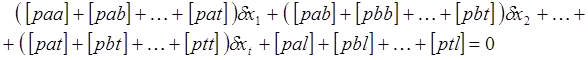
Под заключительными контролями уравнительных вычислений будем понимать контроли, которые охватывают всю совокупность вычислительных операций, начиная с составления нормальных уравнений и кончая вычислением поправок к измеренным величинам. Это контроли, которые по существу должны определять правильность решения параметрических уравнений поправок по методу наименьших квадратов. Обычно они осуществляются сравнением значения суммы [pvv], вычисленной непосредственно с помощью поправок v со значениями [pvv] , полученными по различным формулам метода наименьших квадратов.
Умножим уравнение (28) слева на ![]()
![]()
Принимая во внимание ![]() получим
получим
![]() (49)
(49)
или в поэлементной записи
![]() (50)
(50)
Равенство (50) - это один из наиболее простых заключительных контролей уравнительных вычислений. Он одинаково удобен как для ручного счета, так и для счета на ЭВМ.
Правильность линеаризации параметрических уравнений связи, т.е. правильность вычисления коэффициентов и свободных членов, может быть проверена двумя способами.
Первый из них заключается в том, что поправки к измеренным величинам, вычисленные с помощью уравнений
![]() (51)
(51)
сравниваются с соответствующими поправками, полученными из уравнений связи
![]()
Такой контроль позволяет проверить правильность линеаризации каждого параметрического уравнения. Его обычно применяют при ручном счете.
Второй способ состоит в том, что сумма [рvv] вычисленная с помощью поправок v , полученных из параметрических уравнений связи (51), сравнивается с ее значением, вычисленным по формулам (50). В этом случае контроль линеаризации становятся частью заключительного контроля уравнивания. Этот способ целесообразно применять при счете на ЭВМ.
Как известно, по результатам уравнивания можно оценить точность результатов измерений, что является важной характеристикой качества геодезической сети. Однако такой оценки бывает недостаточно. Для решения задач геодезии необходимо знать точность уравненных элементов геодезической сети. Поскольку элементы геодезической сети являются функциями уравненных параметров, то возникает задача оценки точности такого рода функций.
Оценка точности заданной функции включает в себя такие операции: линеаризацию функции (если функция задана в нелинейном виде), вычисление веса функции (иди обратного веса) и вычисление средней квадратической погрешности функции.
Рассмотрим вопрос о линеаризации функции. Функцию, точность которой оценивается, часто именуют весовой функцией. Пусть задана весовая функция уравненных параметров
![]() (52)
(52)
Подставим в эту функцию вместо параметров их
приближенные значения ![]() , исправленные поправками
, исправленные поправками ![]() .
.
![]()
тогда получим
![]()
Полагая, что ![]() ,
получаемые из уравнивания, достаточно малы, разложим функцию в ряд Тейлора и
ограничимся при этом членами первого порядка
,
получаемые из уравнивания, достаточно малы, разложим функцию в ряд Тейлора и
ограничимся при этом членами первого порядка
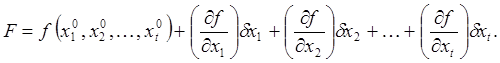 (53)
(53)
Введем обозначения
![]() (54)
(54)
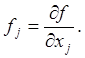 (55)
(55)
Тогда выражение (53) примет вид
![]() (56)
(56)
Введя вектор коэффициентов функции
![]() (57)
(57)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.