Атомная физика
Тепловое излучение
Нагретые тела излучают электромагнитные волны.
Энергетическая светимость тела – поток энергии,
испускаемый единицей поверхности излучающего тела по всем направлениям.
Обозначение: ![]() , где w – частота излучения.
, где w – частота излучения.
Если ![]() , то величина
, то величина ![]() называется испускательной способностью.
называется испускательной способностью. ![]() , где T – температура.
Полная светимость
, где T – температура.
Полная светимость 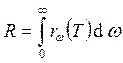 .
.
Пусть на участок тела падает поток ![]() . Тогда
. Тогда 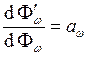 называют
поглощательной способностью тела. Здесь
называют
поглощательной способностью тела. Здесь ![]() –
поглощённая часть потока.
–
поглощённая часть потока. ![]() зависит от температуры,
причём
зависит от температуры,
причём ![]() .
.
Тело, у которого ![]() ,
называется абсолютно чёрным.
,
называется абсолютно чёрным.
Пусть есть
излучающая полость и пусть ![]() – энергетическая
светимость под углом в
– энергетическая
светимость под углом в ![]() . Тогда светимость под углом
. Тогда светимость под углом ![]() – закон Ламберта.
– закон Ламберта.
Излучатели, у которых выполняется закон Ламберта, называются косинусными.
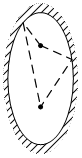 Пусть есть
зеркальная эллиптическая полость, в фокусах которой находятся два излучающих
тела. По свойству эллипса, любой луч, вышедший из одного тела обязательно
попадёт в другое после первого же отражения. Пусть в единицу времени тела
испускают энергию
Пусть есть
зеркальная эллиптическая полость, в фокусах которой находятся два излучающих
тела. По свойству эллипса, любой луч, вышедший из одного тела обязательно
попадёт в другое после первого же отражения. Пусть в единицу времени тела
испускают энергию ![]() и
и ![]() и пусть
и пусть
![]() и
и ![]() –
полные коэффициенты поглощения. Тогда
–
полные коэффициенты поглощения. Тогда 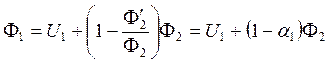
![]() . Т.к. тела находятся в термодинамическом
равновесии, то
. Т.к. тела находятся в термодинамическом
равновесии, то ![]() . Аналогично
. Аналогично ![]() , а
, а 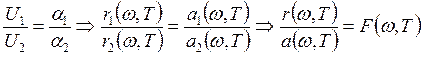 , где
функция
, где
функция ![]() не зависит от природы тела – закон
Кирхгофа.
не зависит от природы тела – закон
Кирхгофа.
Т.к. для
абсолютно чёрного тела ![]() , то
, то 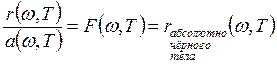 .
.
 Экспериментальная
кривая:
Экспериментальная
кривая:
Для абсолютно
чёрного тела 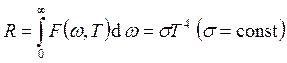 – закон Стефана-Больцмана.
– закон Стефана-Больцмана.
 Оказалось, что
Оказалось, что ![]() , где
, где ![]() – длина
волны, при которой наблюдается максимум функции
– длина
волны, при которой наблюдается максимум функции ![]() – закон
Вина.
– закон
Вина.
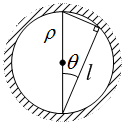
Пусть есть
излучающая сфера и ![]() – поток энергии,
распространяющейся в единичном телесном угле, нормальном к поверхности. Тогда
количество энергии, прошедшей через элементарную площадку
– поток энергии,
распространяющейся в единичном телесном угле, нормальном к поверхности. Тогда
количество энергии, прошедшей через элементарную площадку ![]() в единицу времени
в единицу времени ![]() в
телесном угле
в
телесном угле ![]()
![]() .
Время, за которое излучение пройдёт через сферу в зависимости от угла q:
.
Время, за которое излучение пройдёт через сферу в зависимости от угла q: 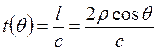 . Тогда
. Тогда 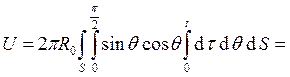
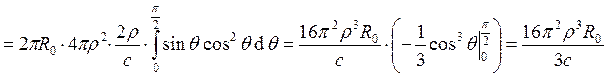 . Плотность энергии в
сфере
. Плотность энергии в
сфере 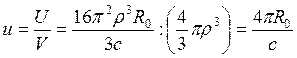 . Т.к. это выражение не зависит от радиуса
сферы, то оно будет верно для любой сколь угодно маленькой сферы. Тогда
плотность энергии в пространстве, равномерно заполненном излучением после
наступления термодинамического равновесия всегда будет равна
. Т.к. это выражение не зависит от радиуса
сферы, то оно будет верно для любой сколь угодно маленькой сферы. Тогда
плотность энергии в пространстве, равномерно заполненном излучением после
наступления термодинамического равновесия всегда будет равна ![]() , где
, где ![]() –
энергетическая светимость излучающего вещества.
–
энергетическая светимость излучающего вещества.
Пусть есть куб
со стороной l. Стоячая волна в нём получится,
если 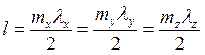 , где
, где ![]() – целые
числа, т.е., если
– целые
числа, т.е., если ![]() , где k
– волновое число. Выясним максимальные значения
, где k
– волновое число. Выясним максимальные значения ![]() и
и ![]() . Стоячая волна будет, если конец вектора
. Стоячая волна будет, если конец вектора ![]() , начало которого пусть лежит в начале
координат, будет лежать в точках, удовлетворяющих этим условиям, в которые
входят также вершины куба. Если изменить, например,
, начало которого пусть лежит в начале
координат, будет лежать в точках, удовлетворяющих этим условиям, в которые
входят также вершины куба. Если изменить, например, ![]() на 1,
приращение волнового вектора будет:
на 1,
приращение волнового вектора будет: 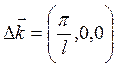 . Объём кубика со
стороной
. Объём кубика со
стороной 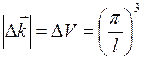 . Конец вектора
. Конец вектора ![]() может
лежать в любой точке сферы радиусом
может
лежать в любой точке сферы радиусом ![]() . Тогда количество
возможных точек, удовлетворяющих вышеприведённым условиям будет:
. Тогда количество
возможных точек, удовлетворяющих вышеприведённым условиям будет: 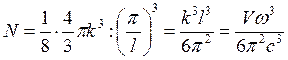 (
(![]() т.к.
нас интересует только первый квадрант);
т.к.
нас интересует только первый квадрант); 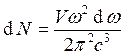 . В
единице объёма
. В
единице объёма 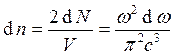 (умножается ещё на два, так как
отличных направлений колебаний электрического вектора два). Таким образом,
(умножается ещё на два, так как
отличных направлений колебаний электрического вектора два). Таким образом, 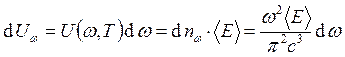 , т.е.
, т.е. 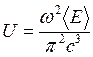 , где E – энергия колебаний.
, где E – энергия колебаний.
Релей и Джинс:
предположим, что осцилляторы в стенке распределены по закону Больцмана: 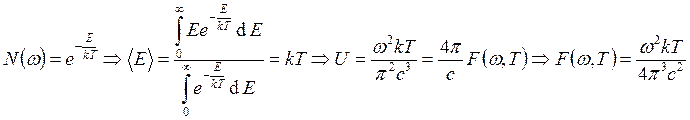 .
.
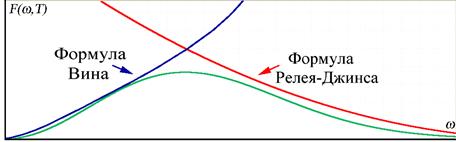 Вин:
Вин: 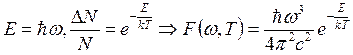 .
.
Планк:
Осциллятор может иметь энергию ![]() , где n – целое число. Вероятность того, что осциллятор имеет
энергию
, где n – целое число. Вероятность того, что осциллятор имеет
энергию ![]() , где
, где 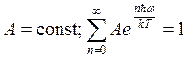 .
.
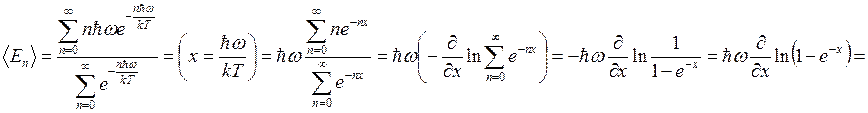
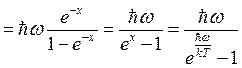 .
.
Отсюда следует, что 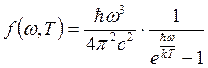 – распределение Планка, которое полностью
описывает эмпирическую кривую.
– распределение Планка, которое полностью
описывает эмпирическую кривую.
Фотоэффект
Явление вырывания электронов с поверхности твёрдого тела под воздействием электромагнитного излучения называется фотоэффектом.
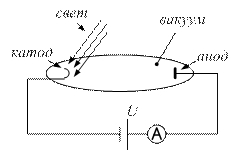
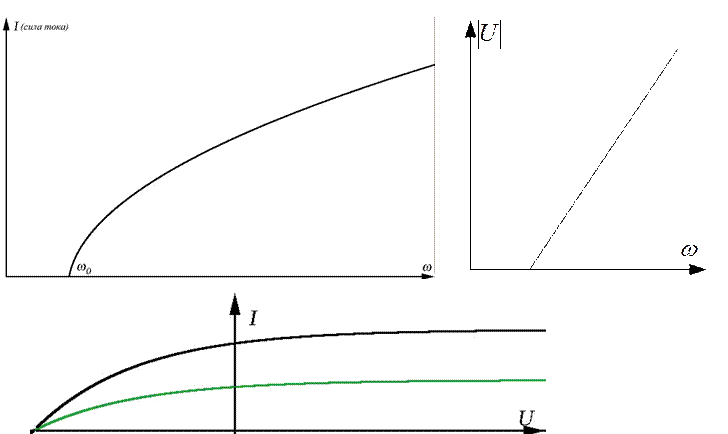
На верхнем левом графике представлена зависимость силы тока от частоты
освещающего света. Видно, что есть минимальная частота, при которой происходит
фотоэффект. Эта частота называется красной границей фотоэффекта.
На верхнем правом графике представлена зависимость модуля приложенного напряжения, необходимого для того, чтобы тока не было, от частоты освещающего света. Модуль потому, что оно отрицательно.
На нижнем графике представлена зависимость силы тока от приложенного напряжения. Видно, что сила тока возрастает до какого-то постоянного значении, которое называют током насыщения. Интенсивность света, создающего ток, сила которого показана зелёным светом, меньше, чем у создающего ток, сила которого показана чёрным цветом.
Закон Столетова: Ток насыщения возрастает вместе с интенсивностью.
Уравнение
Эйнштейна: Электромагнитная энергия переносится
порциями по ![]() и, исходя из закона сохранения энергии в
случае фотоэффекта, можно написать:
и, исходя из закона сохранения энергии в
случае фотоэффекта, можно написать: 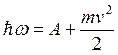 .
.
Энергия фотона ![]() , следовательно, его импульс
, следовательно, его импульс 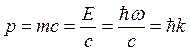 , где k –
волновое число.
, где k –
волновое число.
Эффект
Комптона: Если источник излучает свет с длиной
волны ![]() , то после рассеяния он расщепляется на
свет с длинами волн
, то после рассеяния он расщепляется на
свет с длинами волн ![]() и
и ![]() .
.
Рассмотрим процесс столкновения фотона с электроном:
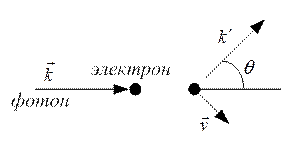
Закон
сохранения энергии: ![]() , где
, где ![]() –
импульс электрона после удара.
–
импульс электрона после удара.
Закон
сохранения импульса: ![]() .
.
![]()
![]() . При этом
. При этом ![]() , следовательно,
, следовательно, 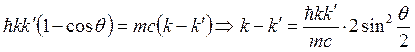 или
или
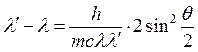 , где
, где ![]() –
постоянная Планка.
–
постоянная Планка.
Эффект Комптона доказывает наличие импульса у каждого отдельного фотона.
Фотон – это физический объект, связанный с электромагнитным
излучением, который взаимодействует с веществом всегда как единое целое. Он
имеет энергию ![]() и импульс
и импульс ![]() . Масса покоя фотона равна 0. От может
существовать только в состоянии движения со скоростью с.
. Масса покоя фотона равна 0. От может
существовать только в состоянии движения со скоростью с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.