Тепловое излучение. Формула Резерфорда. Распределение электронов в атоме по энергетическим уровням. Рентгеновский спектр, страница 3

5.  Невозможно одновременно измерить координату микрочастицы вдоль некоторой оси и проекцию импульса на эту ось. Неопределённость связана соотношением Гейзенберга: .

6.  Новое понимание опыта: произвести опыт над микрочастицей значит изменить её состояние, или Y-функцию.

Математические требования к Y-функции: непрерывность, однозначность и конечность.

Такие значения энергии, при которых Y обладает требуемыми свойствами, называются собственными и  функции от этих энергий тоже называются собственными.

Условие нормировки: .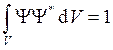

Функция Y определена с точностью до постоянного множителя.

Принцип суперпозиции: если частица может находится в состоянии, характеризуемом функцией  и в состоянии, характеризуемом функцией , то она может находится и в состоянии, характеризуемом функцией . Пусть у частицы есть какая-то измеряемая величина L; в состоянии , в состоянии . Тогда при проведении измерения мы можем с вероятностью  получить в результате , и с вероятностью  – .

Оператор – это правило, которое определяет соответствие между двумя множествами функций, т.е. каждой функции из одного множества ставится в соответствие функция из другого множества. Обозначение: .

1.   – линейный, если .

2.  Если , то .

3.  Если , то .

4.  Вообще говоря, . Если , то операторы называются коммутирующими.

5.  Если , где l – число, то l называется собственным числом оператора , а u – собственной функцией оператора .

6.  Если  (транспонированный и комплексно-сопряжённый), то этот оператор называется самосопряжённым иди эрмитовым.

В квантовой механике используются только эрмитовые операторы.

Основные свойства эрмитовых операторов:

1.  .

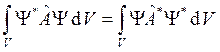2.  Собственные значения эрмитового оператора – действительные числа.

Ортогональность собственных функций

Функции  и  называются ортогональными, есл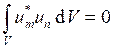и  при . Здесь V – объём, где определены эти функции.

Собственные функции эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг к другу.

Пусть  и  – соответствующие собственные числа. Из основного свойства эрмитового оператора известно, что 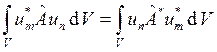. Тогда  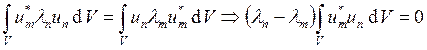и, т.к.  при , то 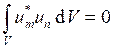, следовательно, функции  и  – ортогональны.

Набор функций таких, что 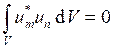 и 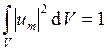 называется ортонормированной системой.

Если  (причём в этом ряде может быть и бесконечное число членов), то u называется полной функцией. При этом .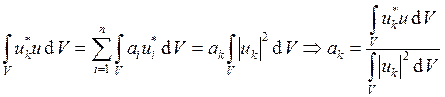

Представление физических величин посредством операторов

Постулаты квантовой механики:

1.  Состояние движения частицы описывается волновой функцией Y.

2.  Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.

3.  При измерении числового значения некоторой физической величины, изображаемой оператором  с определённой вероятностью получается одно из чисел , являющихся собственными числами . Вероятность получения при измерении того или иного значения  вычисляется с помощью следующего правила: Пусть  – собственные функции , т.е. . Функции  представляют собой ортонормированную систему. Разложим Y по . Вероятность того, что при измерении физической переменной, обозначенной  будет получено  равна .

4.  Волновая функция Y подчиняется уравнению Шредингера.

Вычисление средних значений физических переменных: .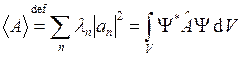

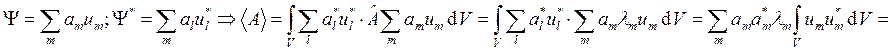
 , т.к. система ортонормированная.

Оператор координаты: 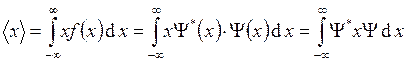 , где  – плотность распределения координаты. Отсюда следует, что оператор координаты сводится к умножению функции на координату:  (в одномерном случае).

Оператор импульса: Проекция оператора импульса на ось x , где  – проекция импульса на ось x. Видно, что 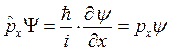 , т.е. оператор импульса .

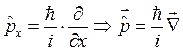Энергия, выраженная через координаты и импульс, называется функцией Гамильтона:   .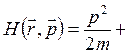

Оператор энергии: .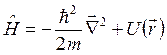

Оператор момента импульса:  .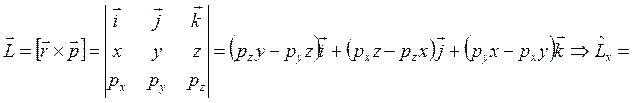

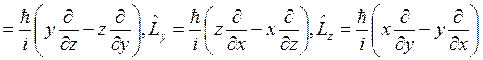Формулы, которые в классической механике служат для связи между численными значениями физических величин, в квантовой механике следует рассматривать как формулы, связывающие операторы этих величин.