Опыт Резерфорда показал, что внутри атома есть заряженная материя, сконцентрированная в маленьком объёме.
Формула Резерфорда
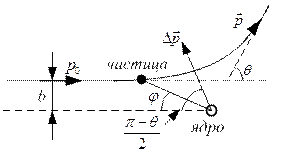 Пусть ядро не
движется. Тогда
Пусть ядро не
движется. Тогда ![]() и
и 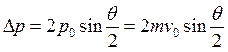 , где
, где ![]() – начальная скорость a-частицы.
– начальная скорость a-частицы. 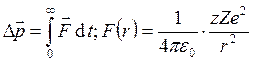 , где z – атомный номер частицы, Z
– атомный номер ядра. Проекция силы на
, где z – атомный номер частицы, Z
– атомный номер ядра. Проекция силы на 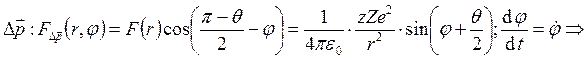
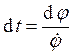 и тогда
и тогда 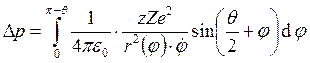 .
Запишем закон сохранения момента импульса:
.
Запишем закон сохранения момента импульса: ![]() и
и 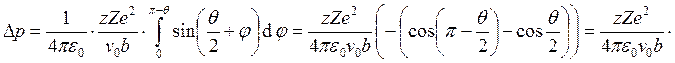
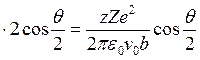 . Таким образом,
. Таким образом, 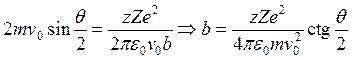 .
.
 Пусть есть мишень
с одним ядром в центре. Тогда на угол q
отклонятся те частицы, которые пролетят на расстоянии
Пусть есть мишень
с одним ядром в центре. Тогда на угол q
отклонятся те частицы, которые пролетят на расстоянии ![]() .
Тогда
.
Тогда 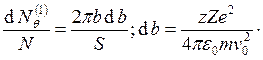
 и
и 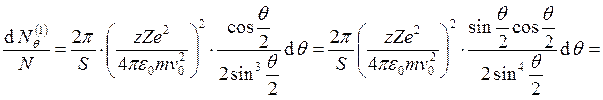
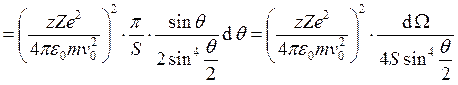 , где
, где ![]() – число частиц, рассеявшихся под углом q (в данном случае на одном ядре), N – общее число частиц,
– число частиц, рассеявшихся под углом q (в данном случае на одном ядре), N – общее число частиц, ![]() –
телесный угол рассеяния,
–
телесный угол рассеяния, ![]() . Знак «–» опущен, т.к.
он несущественен.
. Знак «–» опущен, т.к.
он несущественен.
Пусть теперь
концентрация ядер n, а мишень – толщиной d. Тогда 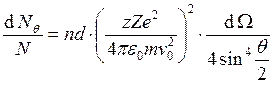 – формула Резерфорда.
– формула Резерфорда.
Экспериментальные закономерности линейчатых спектров
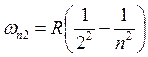 – серия Бальмера.
Здесь R – постоянная Ридберга,
– серия Бальмера.
Здесь R – постоянная Ридберга, ![]() , w
– частота линий спектра;
, w
– частота линий спектра; 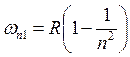 ,
, ![]() – серия Лаймана;
– серия Лаймана; 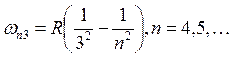 –
серия Пашена.
–
серия Пашена.
Величина  называется спектральным
термом. Остальные серии:
называется спектральным
термом. Остальные серии: ![]() .
.
Комбинационный принцип Ритца: Все наблюдаемые частоты в спектре могут быть представлены в виде комбинации спектральных термов.
Опыт Франка и Герца:
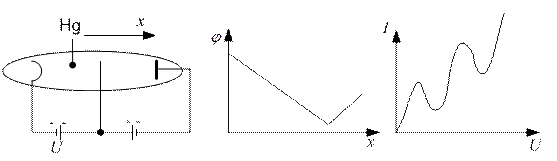
Из опыта Франка и Герца следует, что атом воспринимает энергию порциями.
Постулаты Бора:
1. Среди всех орбит электронов в атоме реализуются не все, а только некоторые, причём если электрон движется по своей орбите, то он не излучает.
2.
Излучение происходит при переходе
электрона с одной орбиты на другую, причём ![]() , где
, где ![]() – энергия электрона на k-й
орбите.
– энергия электрона на k-й
орбите.
Орбиты реализуются такие, что ![]() , где
, где ![]() – радиус n-й орбиты.
– радиус n-й орбиты.
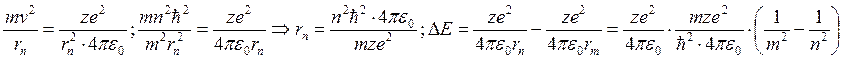 , следовательно, испускаемые частоты
, следовательно, испускаемые частоты 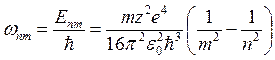 и постоянная Ридберга
и постоянная Ридберга 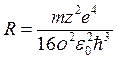 .
.
Волновые свойства частиц
Утверждение де Бройля: Электрон – тоже волновая частица, как и фотон.
Частота электрона 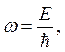 импульс
волновой частицы
импульс
волновой частицы  , следовательно, длина волны
электрона
, следовательно, длина волны
электрона 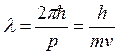 (волна де Бройля). Групповая скорость
электрона
(волна де Бройля). Групповая скорость
электрона 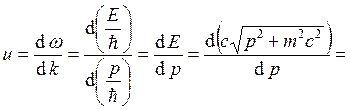
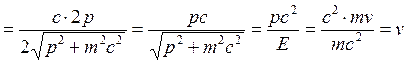 .
.
В опыте
Дэвисона и Джермера поток электронов направлялся на кристалл перпендикулярно
его поверхности и наблюдались максимумы под углами, соответствующими формуле
Вульфа-Брэгга, если положить 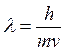 .
.
Сопоставим
частице плоскую волну: ![]() .
.
С точки зрения
волновой теории интенсивность ![]() , где A – амплитуда волны; с точки зрения корпускулярной теории
, где A – амплитуда волны; с точки зрения корпускулярной теории
![]() , где N –
количество фотонов, попадающих на приёмник в единицу времени. Вероятность
нахождения частицы в объёме
, где N –
количество фотонов, попадающих на приёмник в единицу времени. Вероятность
нахождения частицы в объёме ![]() , где
, где ![]() – комплексно-сопряжённая функция для Y.
– комплексно-сопряжённая функция для Y.
Уравнение Шредингера
Пусть ![]() можно представить в виде:
можно представить в виде: ![]() , т.е. частота, а, следовательно, и энергия
колебаний, постоянна. Подставим эту функцию в волновое уравнение:
, т.е. частота, а, следовательно, и энергия
колебаний, постоянна. Подставим эту функцию в волновое уравнение: 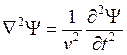 . Т.к.
. Т.к. 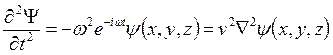 , то
, то 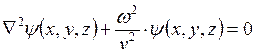 . При этом
. При этом 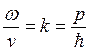 , где p – импульс частицы, энергия частицы
, где p – импульс частицы, энергия частицы 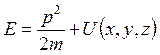 (здесь
(здесь ![]() –
потенциальная энергия частицы) и, следовательно,
–
потенциальная энергия частицы) и, следовательно, 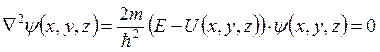 – стационарное уравнение Шредингера.
– стационарное уравнение Шредингера.
Стационарные состояния – такие состояния, которые не зависят от времени.
Принцип неопределённости Гейзенберга:
 Пусть электроны
излучаются вдоль оси y, дифрагируют на щели и
попадают на экран.
Пусть электроны
излучаются вдоль оси y, дифрагируют на щели и
попадают на экран.
Условие минимума:
![]() . Для простоты будем считать, что максимум
у интенсивности только один. Тогда электрон не будет наблюдаться, если
. Для простоты будем считать, что максимум
у интенсивности только один. Тогда электрон не будет наблюдаться, если ![]() . Разложим импульс электрона:
. Разложим импульс электрона: ![]() . Тогда
. Тогда 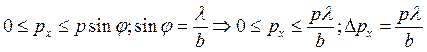 –
интервал, в котором будет
–
интервал, в котором будет ![]() при попадании в
минимум.
при попадании в
минимум.  . Ширину щели можно представить как
погрешность в измерении координаты x электрона.
Тогда
. Ширину щели можно представить как
погрешность в измерении координаты x электрона.
Тогда ![]() – принцип неопределённости Гейзенберга.
– принцип неопределённости Гейзенберга.
Из опыта Бибермана, Фабриканта и Сушкина следует, что отдельные электроны обладают волновыми свойствами.
Итоги:
1. Микрообъекты обладают свойствами одновременно и частиц, и волн и потому не являются ни тем, ни другим в классическом смысле слова.
2. Состояния микрочастиц описываются волновыми функциями. В них свободная частица является плоской волной.
3. Микрочастицы
следует представлять себе размазанными по пространству, причём ![]() характеризует плотность вероятности
нахождения частицы в данном пространстве. Скорость микрочастицы совпадает с
групповой скоростью волн, определяющих её состояние.
характеризует плотность вероятности
нахождения частицы в данном пространстве. Скорость микрочастицы совпадает с
групповой скоростью волн, определяющих её состояние.
4. Микрочастицы не обладают определёнными траекториями в классическом понимании.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.