Тепловое излучение. Формула Резерфорда. Распределение электронов в атоме по энергетическим уровням. Рентгеновский спектр, страница 5

Схема электронных уровней атома водорода:

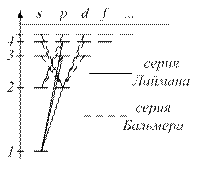Во время перехода момент импульса всегда изменяется на  (правило отбора). Момент импульса фотона равен .

Спектры атомов щелочных металлов

Частоты серий этих атомов: 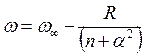 (здесь R – постоянная Ридберга). Для разных атомов и , и a – разное.

Резкая серия: 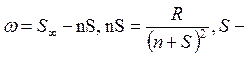 число, .

Главная серия: .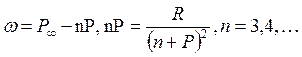

Диффузная серия: .

Основная линия: .

Эмпирически было установлено, что .

Энергия состояния (энергия уровня) зависит не только от главного квантового числа, но и от орбитального (азимутального) квантового числа – это главное отличие атомов щелочных металлов от атома водорода.

Магнитное число определяет проекцию момента импульса на выбранное направление.

Правила сложения моментов импульса

Пусть есть две частицы с моментами импульса  и . Найдём суммарный момент импульса системы . Известно, что . Аналогично и для  и . Т.к. , то проекции их на ось z . При этом .

Нормальный эффект Зеемана

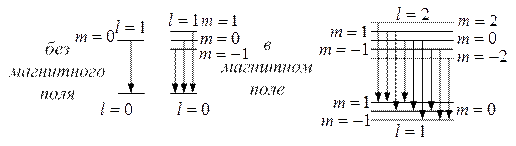
Магнитный момент электрона на орбит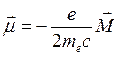е , где  – механический момент, , l – азимутальное квантовое число. Тогда 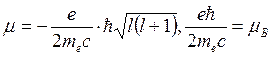 – магнетон Бора. Потенциальная энергия электрона в магнитном поле , где  – напряжённость внешнего магнитного поля. 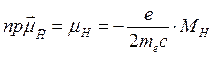. Пусть . Тогда  и 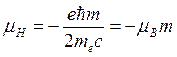, где m – магнитное квантовое число. Таким образом, , следовательно, при помещении атома в магнитное поле его уровни возбуждения расщепляются на  значение (т.к.  через 1), равноотстоящие друг от друга. Магнитное поле снимает вырождение по квантовому числу m.

Правило отбора: . При этом энергии переходов с одинаковым изменением m равны и при  равны энергии перехода без магнитного поля.

Мультиплетность спектров и спин электрона

У щёлочных металлов расщепление линий перехода различно, а  – одинаково.

Мультиплетность – расщепление линий на несколько компонент.

Собственный момент импульса электрона называется спином.

Квантовое число, соответствующее спину – s. Для электрона . Тогда спин электрона 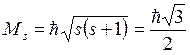. Проекция спина на ось z , где 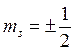 для электрона. Отношение магнитного момента к механическому для электрона: 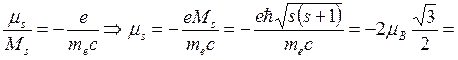 . Знак «–» означает, что . .

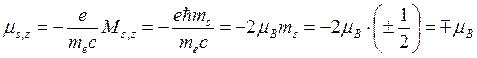Если в атоме один валентный электрон (атом щелочного металла), то полный магнитный момент , где  через 1. Для одного электрона 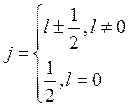. Из-за того, что для уровней, у которых  полный магнитный момент  может принимать два значения, то и магнитный момент будет иметь два значения и состояния с различными значениями j будут обладать различной энергией.

Взаимодействие магнитных моментов электрона и атома называется спин-орбитальным взаимодействием. Им объясняется расщепление линий на две компоненты.

Правило отбора: .

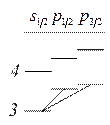Терм – местонахождение атома среди его энергетических уровней.

Обозначение: .

Результирующий момент многоэлектронного атома

Путём сложения всех моментов электрона, как собственных, так и орбитальных, возникает полный механический момент атома. Он получается двумя способами: если в атоме присутствует связь Ресселя-Сандерса, то взаимодействие собственных магнитных моментов и взаимодействие орбитальных моментов электронов сильнее, чем взаимодействие собственных и орбитальных моментов электронов. Тогда 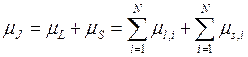, где N – число электронов,  и  –  соответственно орбитальный и собственный моменты i-го электрона. Иначе в атоме присутствует j-j-связь. Тогда 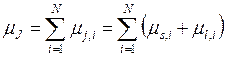. Эта связь встречается реже и свойственна тяжёлым атомам.

Можно представить  так: , где g – фактор Ланде, зависящей от L и S.

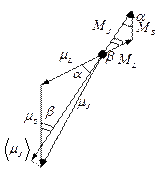Среднее по времени значение полного магнитного момента . При этом  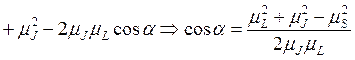. Аналогично 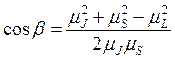. Тогда  .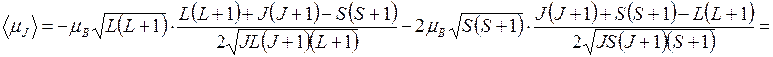

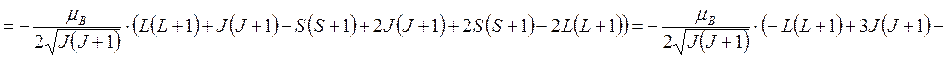
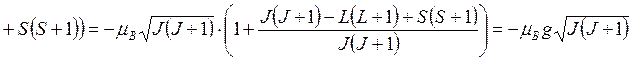Распределение электронов в атоме по энергетическим уровням

Принцип Паули: В одной и той же квантовой системе не может быть двух частиц с полуцелым спином, обладающих одним и тем же набором квантовых чисел.

Состояние электронов в атоме характеризуется числами:  .

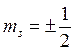Основным состоянием атома является такое, которое обладает минимальной энергией.

Вырождение по числу  для электрона равно . При  – 2 электрона, .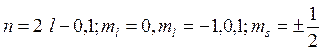

Совокупность электронов, характеризующихся одинаковым главным квантовым числом, называется слоем.