Принцип Гюйгенса. Волновая теория света. Интерференция от тонких пластинок. Дифракционная решётка. Поляризационные призмы и поляроиды

Фотон – это физический объект, связанный с электромагнитным излучением, который взаимодействует с веществом всегда как единое целое. Он имеет энергию  и импульс . Масса покоя фотона равна 0. От может существовать только в состоянии движения со скоростью с.

Ядерная модель атома,формула Резерфорда.

Основанием для построения модели явились опыты по рассеиванию a-частиц  в в-ве. Опыты показали,что осн.часть a-частиц испытывает незначит.отклон-я отпервоначальной троекториипри прохождении тонкого слоя в-ва.однако небольшая часть частиц рассеивалась на очень большие углы(до 180⁰). Это означает,что:  1.отклонение a-частиц обуслов.их взаимодействием с полож.з-ом большой массы.

2.полож.з-д атома сосредоточен в малом объеме, т.к.существ.откл-е испытывают только небольшое кол-во частиц.Модель атома состоит в след.:вокруг полож.ядра с з-дом Ze по замкнутым орбитам движ. Z эл-нов. 1.согласно модели Резенфорда спектры атомов д.б.сплошными,т.е. при переходе эл-на с одной орбиты на другую может испускаться " энергия.

 2.ускор.движ.по отбитам эл-ны должны испускать эл.-маг.волны, при этом терять энергию и в конце концов упасть на ядро.

Пусть ядро не движется. Тогда  и ,

v₀-начальная скорость частицы.

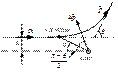
Где z-атомный номер частицы Z-Атомный номер ядра.Прэкция силы :

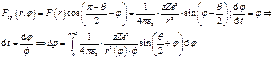
Момент импульса ч-цы в цилиндрич. с-ме коорд. имеет вид:

 

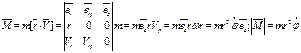
С др. стороны: M=mVb Þ , тогда:

 

Т – кинет. энергия; q₁=2e; q₂=ze. Относительное число частиц dN/N, рассеянное (телесный Ð dW) под Ð рассеивания q к первоначальному направлению дв-я определяется ф-лой Резерфорда:

Эффект Комптона:

Если источник излучает свет с длиной волны λ₀, то после рассеяния он расщепляется на свет с длинами волн λ₀   и λ > λ₀.

Рассмотрим процесс столкновения фотона с электроном:

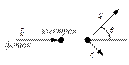Закон сохранения энергии:

где  – импульс электрона после удара.

Закон сохранения импульса:

 

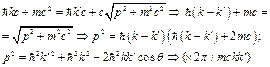
Эффект Комптона доказывает наличие импульса у каждого отдельного фотона.

l₀=2ph/mc{=0,0243 Å} – комптоновская длина волны.(D₀=h/mc=0,00386 Å)

При рассеянии фотонов на эл-ны,связь кот.с атомом велика,обмен эенргией и импульсом происходит с атомом как с целым. Поскольку масса атома намного превосходит массу эл-на,комптоновское смещение получается малым и l’ практически совпадает с l.

Запишем закон сохранения момента импульса:

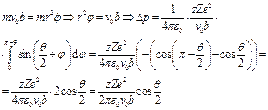
Пусть есть мишень с одним ядром в центре. Тогда на угол q отклонятся те частицы, которые пролетят на расстоянии à

где  – число частиц, рассеявшихся под углом q (в данном случае на одном ядре), N – общее число частиц,  – телесный угол рассеяния, . Знак «–» опущен, т.к. он несущественен. Пусть теперь концентрация ядер n, а мишень – толщиной d. Тогда

Постулаты Бора.Элементарная боровская теория атома водорода

Для объяснения закономерностей в линейчатых спектрах Бор объединил планетарную модель атома Резерфорда с гипотезой Планка о квантовой природе света. Теория атома Бора основывается на двух постулатах:

Let эл-н движ.в иоле атомного ядра с зарядом Ze. При Z=1- это атом водорода,при Z¹1-водородоподобный атом,у кот.удалены все эл-ны кроме одного. Возможны только те орбиты,для кот.мом.импульса уд.усл.:mVr_n=nh. n называют главным квантовым числом. Ур-е движ-я эл-на имеет вид:

Исключая V, получим

. Радиус 1-ой орбиты наз. Боровским. Вн.энергия атома складывается из кин.энергии движ.эл-на и пот.энергии взаим-я эл-на с ядром .

Из ур-я движ.  Þ .

“-“ показывает,что эл-н находится в связанном состоянии. Энерг.состояния при n=1 явл. основными. Для n>1-возбужденные. Е_¥=0 соотв.ионизации атома.

При переходе эл-на из стац.сост-я n₂ в n₁ с меньшей энергией излучается квант

отсюда - пост.Ридберга.

Постулаты Бора

I. Постулат стационарных состояний: В атоме $ стац. состояния, в к-ых он не излучает энергии. Стац. состояниям соответствуют стационарные орбиты электронов, дв-ние по к-ым не сопровождается эл.магн. излучением. При этом значение момента импульса квантованы (принимают только дискретные значения) mVr_n=nħ; r_n – радиус n-орбиты. ħ=h/(2p)

II. Постулат частот: При переходе е^- с одной стационарной орбиты на другую излучается (поглощается) квант излучения с энергией ħw. ħw=E_m-E_n ; if  E_m<E_n поглощение; if E_m>E_n излучение. Постулаты бора были подтверждены Франком и Герцем.

Опыты Франка и Герца

Их опыты подтверждают существование дискретных энергетических уровней атома. Схема их установки:

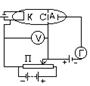
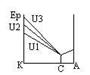
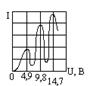
В трубке, заполненной парами ртути под не> P (1гПа) имелись 3 электрода: К, Сетка, А. e^-, вылетающие из К ускоряются разностью потенциалов U, между К и С. U м. плавно менять с help Потенциометра. Между С и А создавалось слабое эл.поле, тормозившее дв-ние е^- к А. На рис.2 показано изменение потенц. энергии е^- Е_р=-еj в зазоре му электродами при различных значения U му К и С (j - потенциал в соответствующей т. поля). Исследовалась зависимость I в цепи А от U му К и С. Сила тока измерялась Гальванометром, напряжение – вольтметром. I монотонно возрастала, достигая max, потом резко падала, достигая min, и снова начинала расти.

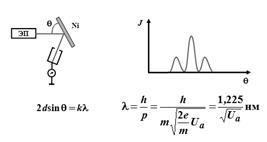
Опыты Дэвиссона и Джермера

Плоская волна де-Бройля

Сопоставим частице плоскую волну:

С точки зрения волновой теории интенсивность, где A – амплитуда волны; с точки зрения корпускулярной теории , где N – количество фотонов, попадающих на приёмник в единицу времени. Вероятность нахождения частицы в объёме , где  – комплексно-сопряжённая функция для Y.

Волновая ф-ция

Max-ы в дифракционной картине соответствуют наи> интенсивности волн де Бройля, с др. стороны, интенсивность  max там, где наибольшее число ч-ц, т.е. ч-цы с > вер-тью оказываются в тех местах, где интенсивность max. Поэтому " описания дв-я ч-ц вводят волновую ф-цию Y. ÷Yç² – наз. амплитудой вер-ти. С help Y-ф-ции м оценить вер-ть того, что ч-ца в момент времени t находится в объеме dV.

 - параллелепипед

dP=÷Y(x,y,z)ç²dV, при этом ÷Yç²=dP/dV – плотность вер-ти., т.е. вер-ть нахождения ч-цы в ед. объеме.

Волновая ф-ция подчиняется условию нормировки:

 - Это вер-ть нахождения ч-цы в какой-либо точке ¥ пространства Þ событие достоверное.

Стандартные условия, налагаемые на волновую ф-цию: в соответствии со своим смыслом волновая ф-ция д.б. однозначной, непрерывной, конечной, д. иметь непр. и конечную производную

Такой ход кривой объясняется тем, что вследствие дискретности энергетических уровней атомы могут воспринимать энергию только порциями DЕ₁=Е₂-Е₁, DЕ₂=Е₃-Е₁, Е_i – энергия i-ого стац. состояния. До тех пор, пока энергия < DЕ₁, соударения му е^- и атом носят упругий характерр..

Часть е^- попадает на С, остальные на А, создавая ток в цепи Г. Чем > V, с к-ой е^- достигают С (чем >U), тем > будет доля е^-, проскочивших С, и Þ будет > I. Когда энергия, накапливаемая е^- в пространства К-С, достигнет DЕ₁, соударения будут неупругими – е^- при ударах об атомы передают им энергию DЕ₁ и продолжают двигаться с <V. Þ <I. Атомы, получившие при соударении с е^- энергию DЕ₁, переходят в возбужденное состояние, из к-ого возвращаются в основное, излучая фотон с частотой w=DЕ₁/ħ. При U=9,8В, е^- на пути К-А м. дважды претерпеть неупругое соударение с атомами ртути, теряя при этом энергию, всдледствие чего сила тока уменьшается. При еще большем U возможны трехкратные неупругие соударения, что приводит к возникновения max. Т.о., непосредственно обнаруживается $ у атомов дискретных энергетических уровней

СВОЙСТВА ВОЛН ДЕ БРОЛЛЯ.

1.фазовая скорость:

.

Эта вел=на имеет чисто символич.значение и относится к разряду принципиально ненаблюдаемых величин.

2.групповая скорость:

Дисперсия света-зависимость пок-ля преломления в-ва или фазовой скорости света в среде от длины световой волны. n=f(l₀)

Дисперсия в-ва D=dn/dl- показывает как быстро меняется пок-ль преломления сдлиной волны.

Суперпозиция волн с частотами,заключ.в небольшом интервале Dw наз.волновым пакетом. Энергия группового пакета сосредоточена в небольшом интервале частот,поэтому его наз.также импульсом света.

Групповая скорость-ск-ть движ-я max огибающей амплитуд группы волн или скорость движ-я цетра пакета.

 

-скорость частицы.

3.волны де Бролля испытывают дисперсию,что приводит к быстрому расплыванию пакета или разделению его на несколько частей в то время,когда частицы постоянны.

Стандартные условия,налагаемые на волновую функцию:

1.Y д.б.непр.,однознач.,конеч.во всех точках пр-ва.

2.if пот.энергия U(x,y,z) имеет пов-ти разрыва,то на таких пов-тях Y и ее первая производная д.оставаться непр.

3.в обл.пр-ва,где U обращ.в ¥,Y д.б.равна 0,причем в силу непр-ти на границе этой обл.Y д.также обращаться в 0.

4.½Y½²-интегрируема.

Для движения частицы в стац.поле U(x,y,z) имеет смысл пот.энергии. В этом случае решение ур-я Шредингера распадается на 2 сомножителя,один из кот.зависит только от коорд.,а 2-ой-от времени. ,

y-подчиняется ур-ю Шредингера для стац.сост-ий,Е-полная энергия. .

Волны де Бройля.

Согласно гипотезе де Бролля " частицы материи обладают наряду с карпускулярными св-вами также и волновыми. С каждым микрообъектом связывается карпускулярн. Энергия и импульс и волновые частота длина волны,кот.связаны между собой : Е=hw и р=2ph/l ,l-длина волны де Бролля.

Гипотеза была подтверждена экспериментально: при рассеянии эл-нов на кристалле и прохождении их ч-з мет.фольгу наблюдалась дифракц.картина. Та же картина наблюдалась при прохождении эл-нов ч-з кристалл по одиночке. Þ Волновые св-ва присущи каждой отдельной частице.

Утверждение де Бройля: Электрон – тоже волновая частица, как и фотон.

Частота электрона  импульс волновой частицы , следовательно, длина волны электрона  (волна де Бройля). Групповая скорость электрона  .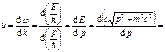

В опыте Дэвисона и Джермера поток электронов направлялся на кристалл перпендикулярно его поверхности и наблюдались максимумы под углами, соответствующими формуле Вульфа-Брэгга, если положить .

Принцип неопределенности Гейзенберга " координат и импульсов.

Из-за наличия волновых св-в у микроч-ц к ним не применимо понятие траектории. В частности нельзя одновременно точно определить координату и импульс ч-цы. Пусть поток эл-тов проходит чз узкую щель шириной Dх. На экране наблюдается дифракционная картина. Из-за этого появляется неопределенность в значении

Р_х. 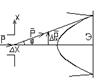DР_х=Psinj=2πħsinj /l. Угол дифракции l определяется условием I min, т.к. центральный max имеет наибольшую интенсивность, это означает, что ч-цы с наи> вер-тью д. попадать именно в обл. центрального max. Dх sinj=l, тогда  Dх DР_х=h, где h=2πħ. Т.к. незначительная часть е^- рассеивается под Ð, " к-ых DР_х>Psinj, то Dх DР_х³h – принцип неопределенности. В общем виде принцип неопределенности: произведение неопределенностей коорд-ты на соответствующие им неопределенности импульсов не м.б. < h.  Dх DР_х³ħ/2 ;

Dу DР_у³ħ/2 ; Dz DР_z³ħ/2; ħ/2 – min значение, к-ое получено. 

Dх DV_х³h/m. Чем > масса, тем < неопределенность в определении координаты и V, if коорд. ч-цы определены с точностью до ее размеров Dх, а масса достаточно велика, то м. оказаться, что DV_х<<V и тогда к описанию дв-ия ч-цы м. применить корпускулярный подход, т.е. определить ее траекторию. Ех, при дв-ии е^- в ЭЛТ м говорить о траектории, а при дв-ии его в атоме нельзя.

 Соотношение неопределенностей " энергии и времени. DEDt³h. С-ма, имеющая время жизни Dt не м.б.  охар-на определенным значением энергии. Разброс в значениях энергии.  DE=h/Dt возрастает с < среднего времени жизни ч-цы. Частота излученного фотона Dn=DE/h также имеет неопределенность. Это подтверждено экспериментально. Спектральные линии размыты, измеряя их ширину м. оценить время жизни атома в возбужденном состоянии.

Собств. ф-ции, значения. Ортогональность. Полнота.

Оператор – это правило, с help к-ого каждый