Определение скорости полёта пули с помощью баллистического крутильного маятника

Лабораторная работа №9

Определение скорости полёта пули с помощью баллистического крутильного маятника.

группа Э-1-03

                                                                                                 Выполнил: Бондарев Д.И.

                                                                                             Проверил: Маркин А.П                                                                                                                                                                                                                                                                                                                                                                                       

Обнинск 2003г.
Цель работы: Определить скорость полета пули с помощью баллистического крутильного маятника.

Приборы и материалы: Баллистический крутильный маятник, пуля в форме полого цилиндра.

Выполнение:

Упражнение 1.

№	L,мм	Φ,град	Φ0,рад
1	114	7	0,122
2	110	6	0,105
3	112	8	0,140
4	114	6	0,122
5	110	8	0,105
6	105	7	0,122
7	111	6	0,105
8	115	7	0,122
9	113	6	0,105
10	120	7	0,122

Перевод значения для угла из градусной меры в радианы:

Φ₀ = Φ*π/180

1)  Φ₀=0,122

2)  Φ₀=0,105

3)  Φ₀=0,140

4)  Φ₀=0,122

5)  Φ₀=0,105

6)  Φ₀=0,122

7)  Φ₀=0,105

8)  Φ₀=0,122

9)  Φ₀=0,105

10) Φ₀=0,122

Вычисление средних значений длины и величины угла:

<X>= 1/n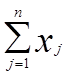

<Φ₀>= 0.33 {рад}

<L>= 119 {мм}

Определение средних квадратичных погрешностей  единичных измерений:

S_n=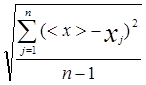

S_φn=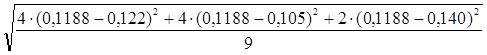=0,014 рад

S_Ln=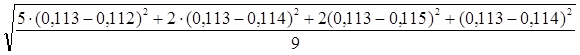=0,0013

Определение средних квадратичных погрешностей средних значений :

S_L=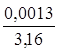=0,0004

S_φ=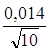=0,0044

Вычисление абсолютных погрешностей:

∆х=

∆x_cл=t_α,n∙S (a=0,95; t_a,n=2,3)   

Dx_слf=0,0044×2,3=0,01 рад

Dx_слL=0,0004×2,3=0,00092 м

DL==0,05

Df₀==0,0007

Второй этап эксперимента не меняет положений грузов R₁. Отклонить маятник на угол 15-17 градусов и отпустить. Убедиться. Что стержень пресекает луч фотодатчика. Далее по показаниям мили секундомера вычислить период колебания T=t/n. Проверить изменение T при других положениях грузов.

Упражнение 2.

№	T1	T2
1	20,850	19,113
2	20,842	19,120
3	20,861	19,140
4	20,834	19,153
5	20,833	19,156
6	20,920	19,114
7	20,844	19,211
8	20,836	19,123
9	20,821	19,118
10	20,831	19,119

<Dt1>=20,847 с

<Dt2>=19,137 с

Dt_сист=0,005 с

S_n=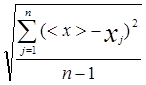

S_nt=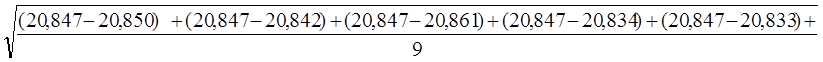

=

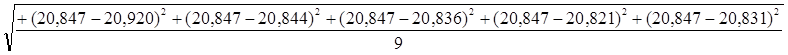=0,028

S_nt=

=0,031

Определить среднеквадратичные погрешности средних значений t₁ и t₂:

S=S_n/ с

St₁=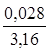=0,009 с

St₂=0,01 с

Определить абсолютные погрешности средних значений t₁ и t₂:

Х_сист=t_a×S  (a=0,95; t_a,n=2,3)

Х_сист,t1=2,3×0,009=0,0207 с

Х_сист,t2=2,3×0,01=0,023 с

Dt₁==0,0213

Dt₂==0,02

Вычислить среднее значение пули по формуле:

m=0,000815 кг – масса пули

M=0,18130,0001 кг  - масса груза

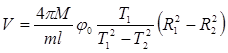
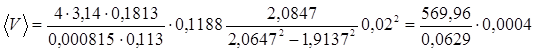
 м/с

Оценим вычисления погрешности скорости пули:

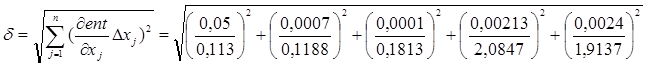
 м/с

 м/с

Вывод:

В результате проведенных опытов мы нашли скорость пули. Анализируя результат, видим, что такая скорость пули в данных условиях возможна. Следовательно, при проведении работы не было допущено грубых измерительных и вычислительных ошибок.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Абсолютно неупругое взаимодействие – это взаимодействие, в результате которого обе частицы «слипаются» и далее движутся как единое целое(или это взаимодействие,после которого тела имеют одну и ту же скорость или покоятся).

Абсолютно упругое взаимодействие – это столкновение в результате которого внутренняя энергия частиц не меняется, а поэтому не меняется и кинетическая энергия системы.

2. Измеряя параметры движения баллистического маятника после удара, можно определить величины, характеризующие тело или явление создавшее это воздействие. На этих принципах основано определение скорости полета пули при помощи баллистического маятника.

3. Моментом импульса материальной точки А относительно точи О называют вектор, равный векторному произведению радиус-вектора, характеризующего положение точки относительно точки О выбранной системы отсчета, и импульса этой точки в этой системе.

Моментом импульса твердого тела А относительно точи О называют вектор, равный сумме векторных произведений радиус-векторов элементарных частиц, характеризующих положение тела относительно точки О выбранной системы отсчета, и импульсов элементарных частиц тела в этой системе.

Моментом силы относительно точки О называют вектор, равный векторному произведению радиус-вектора и силы.

Моментом инерции называют отношение суммы проекций внешних сил, приложенных к телу, на неподвижную ось вращение к угловому ускорению тела.

4.

5. Теорема об изменении момента импульса тел:

Момент импульса системы может изменяться под действием только суммарного момента всех внешних сил.

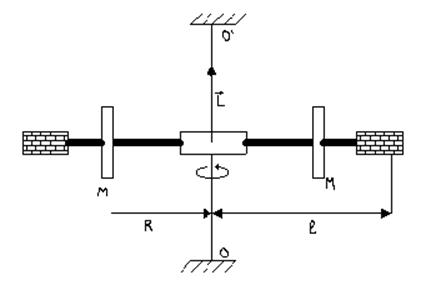
Время удара   значительно меньше периода колебаний маятника T. За время   маятник не успевает существенно отклониться от положения равновесия; в этом случае момент упругих сил, возникающих при повороте маятника, можно пренебречь. Следовательно, момент импульса системы пуля-маятник во время удара сохраняется. Тогда можно записать:

(I1+ml²)ω-mVl=0                (1)

где первый член в уравнении описывает момент импульса системы после удара, второй-до удара; I1 и ml² -моменты инерции маятника и пули относительно оси OO(l -расстояние от места попадания пули в мишень