Выполнение работы.
Упражнение №1. Определение момента инерции маятника.
1. ажав на кнопку «Пуск» на секундомере проверить отсчет времени t – 10 раз. Результат измерений занести в таблицу №1.
Таблица№1.
|
Сменные кольца,г |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
t7 |
t8 |
t9 |
t10 |
|
389,4 |
1,949 |
1,966 |
1,950 |
1,968 |
1,950 |
1,968 |
1,951 |
1,968 |
1,949 |
1,961 |
|
257,3 |
1,878 |
1,896 |
1,874 |
1,896 |
1,876 |
1,896 |
1,880 |
1,889 |
1,880 |
1,900 |
Для m=389,4г Для m=257,3г
<t>=1,958с <t>=1,887с
Вычисление по формуле 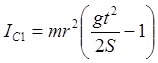 момент
инерции маятника по данным экспериментальным результатам r-радиус
валика, r=0,5см
момент
инерции маятника по данным экспериментальным результатам r-радиус
валика, r=0,5см
Для m=389,4г=0,3894кг
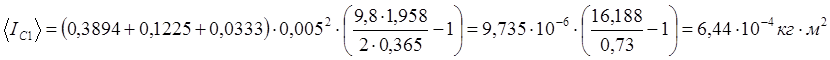
Для m=257,3г=0,2573кг
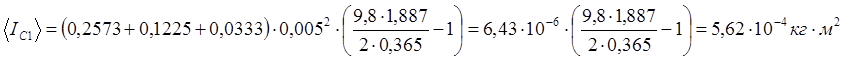
Теперь расчитаем абсолютную и относительную погрешность.
![]() ;
; ![]() ;
; ![]()
Для t рассчитаем относительную погрешность (для m=389,4г).
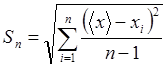 ;
;
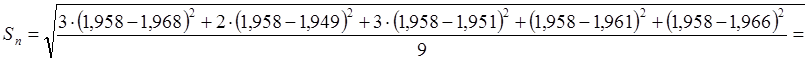
![]()
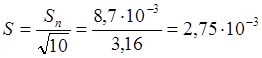
![]()
![]()
![]()
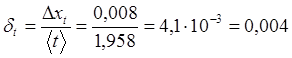
Для m=389,4г
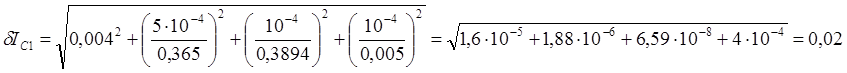
Для 389,4г
![]()
Для 389,4г ![]()
Аналогичные операции повторим для времени с массой сменного кольца равной m=0,2573кг
Dr= 10-4м
Dm=10-4кг
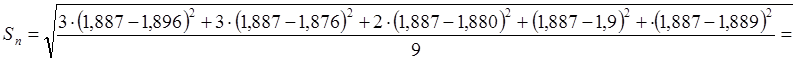
![]()
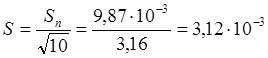
![]()
![]()
![]()
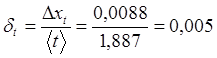
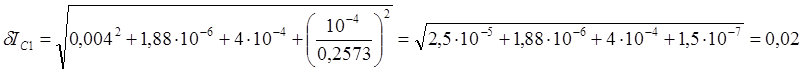
![]()
Для m=0,2573кг ![]()
Упражнение №2. Измерение диаметров валика, диска, сменного кольца и рассечет момента инерции маятника.
1. Измерим штангенциркулем диаметры указанных выше тел. db=1см; dg=8,6см;dk=0,9см
2. Теперь рассчитаем момент инерции IC2 маятника и оценим погрешность.
![]()
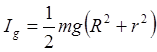
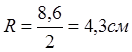 r=0,5
r=0,5
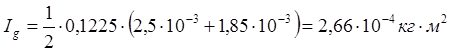
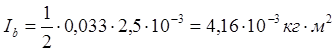
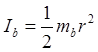
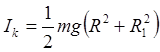 , где R1=0,45, R=4,3см.
, где R1=0,45, R=4,3см.
![]()
![]()
![]() для m=389,4г
для m=389,4г ![]() для m=257,3г
для m=257,3г
Для ![]() для m=389,4г рассчитаем абсолютную погрешность:
для m=389,4г рассчитаем абсолютную погрешность:
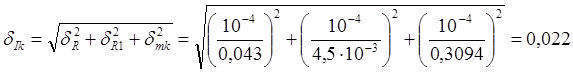

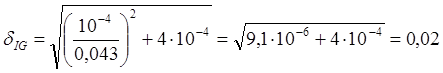
![]()
![]()
![]()
Для ![]() для m=257,3г
для m=257,3г
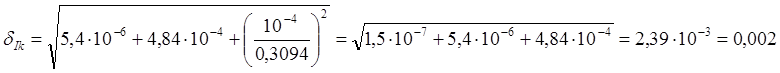
![]()
![]()
![]()
![]()
![]()
Вывод: Изучил плоскопараллельное движение твёрдого тела на примере маятника Максвелла и рассчитал момент инерции маятника двумя способами (все необходимые вычисления и расчётные формулы для нахождения момента инерции маятника двумя способами приведены выше).
Контрольные вопросы.
1. Такое движение твёрдого тела, при котором все точки описывают траектории лежащие в параллельных плоскостях.
2. Такое движение описывается двумя уравнениями динамики:
· Уравнением динамики центра масс
![]() (сумма внешних сил приложенных к телу)
(сумма внешних сил приложенных к телу)
· Уравнением моментов (для описания вращательной состовляющей плоского движения)
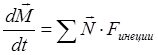
3. Ось проходящая через центр масс тела, которая может служить свободной осью.
4.
Уравнение моментов относительно
оси, проходящей через центр масс твёрдого тела (выбран центр масс). В этом
случае сумма моментов сил равна 0. Уравнение моментов принимает в этом случае
такой же вид как и относительно оси, не имеющей ускорение. 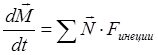
![]()
6.
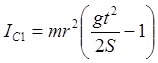
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.