Определение момента инерции гироскопа относительно оси собственного вращения

Теория

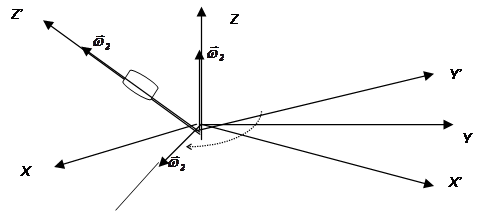
Гироскопом называется твердое тело, быстро вращающееся вокруг своей оси симметрии, соответствующей максимальному осевому моменту инерции. Движение гироскопа – пример движения тела, имеющего только одну закрепленную точку. Такое движение в каждый момент может рассматриваться как вращение вокруг оси, проходящей через эту точку. Если положение твердого тела относительно неподвижной системы отсчета задавать углами Эйлера  (рис.1), то мгновенная угловая скорость   тела может быть представлена как сумма:

                                    = ₁ + ₂  + ₃ ,                                                                    (1)

где    ₁ = - скорость собственного вращения вокруг оси симметрии тела; ₂ =  -  скорость прецессии; ₃ =  -  скорость нутации;

Рис.1

OXYZ – неподвижная прямоугольная система координат; OX’Y’Z’  - жестко связанная с телом прямоугольная система координат;ON – линия узлов (линия пересечения плоскостей XOY и X’O’Y’);j - угол собственного вращения;Y - угол прецессии;q - угол нутации.

При этом вектор угловой скорости меняет свое положение как относительно неподвижной системы отсчета, так и относительно самого тела.

 Описание поведения гироскопа основано на применении уравнения моментов:

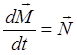                                                                                                                            (2)

где - момент импульса гироскопа относительно закрепленной точки О;

       - сумма моментов сил относительно той же точки.

Заметим, что в общем случае движения момент импульса не совпадает  по направлению ни с вектором угловой скорости , ни с одним из направлений, отмеченных на рис.1

Однако если гироскоп вращается очень быстро  вокруг своей оси симметрии, то есть:

                                                   w₁ >> w₂    и   w₁ >> w₃ ,

то вектор угловой скорости   и вектор момента импульса практически совпадают с направлением оси симметрии гироскопа OZ’.

На этом основании в элементарной теории гироскопа делается допущение, что момент импульса  направлен вдоль оси собственного вращения гироскопа.

Если гироскоп уравновешен, то его центр масс совпадает с неподвижной точкой О и, следовательно, сила тяжести не создает относительно точки О момента, а моментами сил сопротивления можно пренебречь и тогда согласно (2)

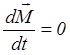
и момент импульса должен оставаться постоянным. В этом случае ось симметрии быстро вращающегося гироскопа сохраняет свое направление относительно неподвижной системы координат.

Если ось гироскопа подвергнуть кратковременному воздействию (ударить), то  момент импульса получит малое приращение

                                                            ,

после чего ось гироскопа будет совершать быстрые колебания с малой амплитудой около своего среднего положения. Такое движение оси гироскопа называется нутацией.

Если же на ось гироскопа действует момент внешних сил, то наблюдается движение оси, называемое прецессией.  В соответствии с основным допущением элементарной теории считаем, что момент импульса гироскопа направлен вдоль оси собственного вращения и может быть выражен формулой:

                                                            ₁,                                                                (3)

где I – момент инерции гироскопа относительно оси OZ’.

Если на ось гироскопа действует сила , то создаваемый ею момент сил  относительно точки О за время  сообщит моменту импульса приращение , направленное перпендикулярно оси гироскопа. Это приращение вызывает поворот оси гироскопа в направлении .

Если сила продолжает действовать, то конец вектора должен описывать окружность в плоскости, перпендикулярной к оси OZ, а ось гироскопа будет прецессировать вокруг оси OZ, занимая в пространстве последовательность позиций, образующих конус прецессии.

       Выведем выражение для скорости прецессии. По определению:

                                                          w_{2  = .}

Как видно из чертежа,

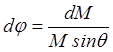
и для скорости прецессии с учетом (2) и (3) получим

                                                       w_{2 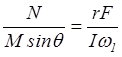 =}                                                                                     (4)

                                                        Выполнение работы.

Упражнение 1.

Проверка формулы для скорости прецессии

При постоянной скорости собственного вращения проверить справедливость соотношения, вытекающего из (4):

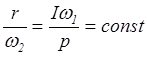                                                                                                                (5)

Здесь положено  F = P, поскольку единственной силой, действующей на ось гироскопа является сила тяжести.

Упражнение предлагается выполнять в следующем порядке.

1.  Установить скорость вращения двигателя = 5000 об/мин.

2.  Найти положение  равновесия  гироскопа.   Для   этого   необходимо   установить

такое положение противовеса (4), при котором прецессия отсутствует. Это и будет положение равновесия. Измерения провести не менее пяти раз, причем для каждого нового измерения необходимо вывести гироскоп из положения равновесия, полученного в предыдущем измерении.