Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций

Б1. 1. Постановка задачи об  интерполяции функций. Интерполяция многочленами

Пусть на отрезке [а,b] имеется произвольная совокупность различных n+1 точек a=х₀,х₁,...х_n=b называемых узлами, а совокупность узлов есть сетка. В каждой точке х_i задано значение исходной функции f(X_I). Пусть задан набор функций φ_k(х),

k = 0, 1,...,n, с помощью которых можно построить линейную комбинацию вида:

Если в узлах φ(х_i)=f_i, т.е.

то говорят, что функция φ (х) интерполирует F(х).

Схема Чебышова

Выражение (2) есть система n+1 одного уравнения с n+1 неизвестными a_k. Чтобы эта задача была разрешима, необходимо выполнение двух условий. Во-первых, система функций φ_k(х),должна быть линейно-независимой, в противном случае в этой сумме число параметров а_к может быть сокращено. Во-вторых, для разрешимости системы (2) по теореме Крамера необходимо и достаточно, чтобы следующий функциональный определитель был отличен от нуля.  Интерполяционный многочлен строится по какой-либо чебышевской системе функций.

 где Δ_ij - алгебраические дополнения элементов i-го столбца. Подставляя а_i  в (1), получаем выражение для интерполирующей функции.

Метод Монте-Карло Вэтом методе интегралы вида ,

 

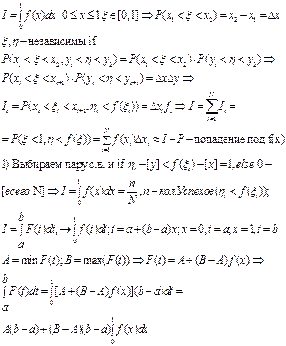
Чаще всего точная величина а неизвестна, и тогда вводят предельную абсолютную погрешность Δ_а, которую определяют как всякое число, не меньшее абсолютной погрешности

Погрешность результата арифметической операции с приближенными числами.

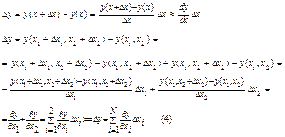
Т1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел.

Доказательство. Пусть  - приближенные числа. Рассмотрим алгебраическую сумму y = ±x₁±x₂±…±x_n (5)

Формулу (5) будем рассматривать как функцию n переменных. Очевидно, что. Используя (4), получим:

Δy = ±Δx₁ ± Δх₂ ±… ± Δх_n à |Δy| ≤ |Δx₁ |+ |Δх₂ |+… +| Δх_n|

Что и требовалось доказать.

Теорема Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.

Это и есть обобщенный интерполяционный многочлен для функции f Поскольку для f должно выполняться условие в узлах

то функция Ф_j ,(х_i) обладает свойством

Интерполяционный многочлен логранжа

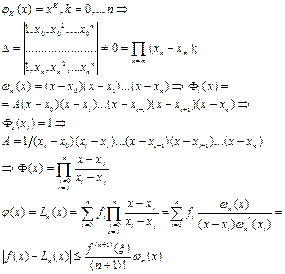
Второй способ вычисления, заключается в том, что интеграл рассматривается как математическое ожидание от случайной функции f с равномерной плотностью распределения от равномерно распределенной величины х.

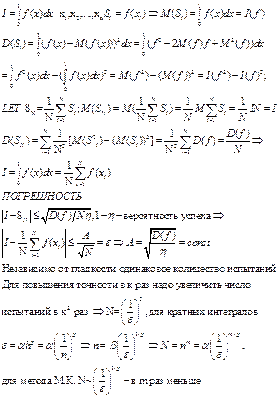
Доказательство.

Пусть à

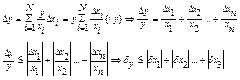
Теорема. Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

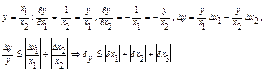
Первый, заключается в отбрасывании знаков числа, количество которых превышает количество разрядов п, с которым работает машина. Если мы хотим удержать в числе первые п знаков, и в следующем (n +1) разряде стоит цифра а_n+1 > 5, то к п разряду добавляется единица. В противном случае цифра n -го порядка остается без изменений.

Определение. Первые n значащих цифр (знаков) верные, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого п- значащей цифрой. Это означает, что если известно, что в записи числа

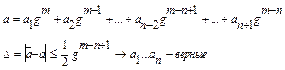
Интерполяционный многочлен Ньютона

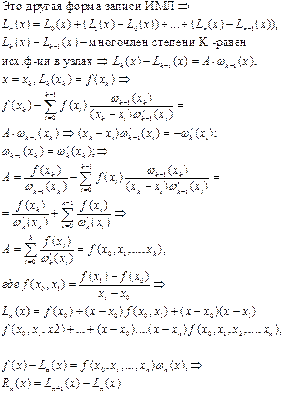
Б2.

1. Числа, представление чисел, рациональные и иррациональные числа, округление, ошибки округления

Определение. Число - это определенным образом упорядоченная последовательность цифр. Действительное число единственным образом представляется в виде бесконечной суммы

Здесь a_i - цифры, а_n ≠ 0, n — целое. Число g > 0 называется основанием системы счисления. При этом 0≤a_i≤g-1à

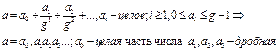 Определение.   Если в дробной части формулы (3) последовательность цифр начиная с а_к является повторяющейся, т.е.

то такое число называется рациональным. Рациональное число может быть представлено в виде

Если в бесконечной последовательности нет периодически повторяющейся последовательности, то число иррационально. Замечание. Все системы счисления используют для записи чисел некоторое количество цифр, по крайней мере, цифры 0 и 1 содержат все системы. Поэтому, до тех пор, пока не указана система счисления, не определено и значение числа.

Определение. Погрешностью определения (записи) числа а является разность между приближенным значением а и точной величиной а:.

Определение. Абсолютной погрешностью числа а называется модуль Δa

Определение. Относительная погрешность есть отношение абсолютной погрешности к модулю числа

2. Сплайны, простейшие сплайны, построение сплайна