Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций, страница 6

простейшая одночленная формула для первой производной является формулой первого порядка точности.

Рассмотрим теперь формулу второй производной (10). представим первое слагаемое правой части в виде разложения по формулу Тейлора в координате одного из узлов. Рассмотрим производную в окрестности точки х₀, левой точки промежутка

[х₀, x₂]. Для этого нужно разложить f₁; и f₂  B окрестности точки х₀

Б12.

1. Формулы прямой и обратной прогонки

МЕТОД ПРОГОНКИ

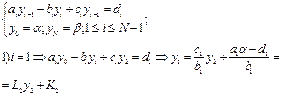
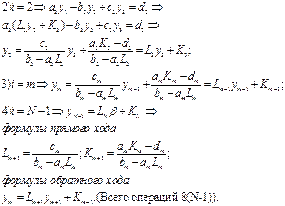
и эти равенства дают 2N соотношений для определения неизвестных констант а_i, и b_i

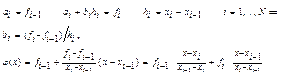
и в точности совпадает с интерполяционным многочленом Лагранжа в том случае, когда интерполяция проводится по двум точкам. Но в отличие от линейной лагранжевой интерполяции, с помощью сплайновой технологии можно аппроксимировать и неоднозначные кривые.

Интерполяция кубическими сплайнами

Если обозначить через у(х) отклонение от положения равновесия на каждом промежутке между узлами, то условием равновесия линейки является соотношение

Отсюда получаем, что кривая между соседними узлами имеет следующий вид: у(х) = А + Вх + Сх² +Dx³.y”(x0)=0,y”(N)=0

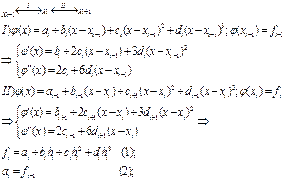
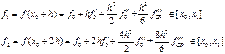
Как и в случае формулы (9) мы предполагаем, что исходная функция обладает необходимым количеством производных для представления ее по формуле Тейлора. Тогда имеем

одночленная формула второй производной тоже является формулой первого порядка точности. Определим теперь погрешность в среднем узле промежутка х₁. Для этого нужно разложить f₀ и  f₂в окрестности этой точки:

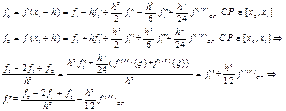в средней точке промежутка погрешность оказалась пропорциональной не первой степени h, а квадрату шага h²-второй порядок точности формулы (10) в средней точке интервала.

Двучленные формулы численного дифференцирования для получения формул численного дифференцирования используем первые два слагаемых.

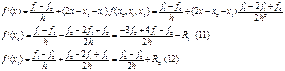
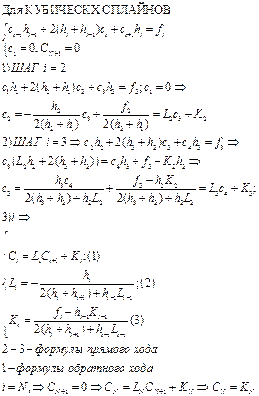
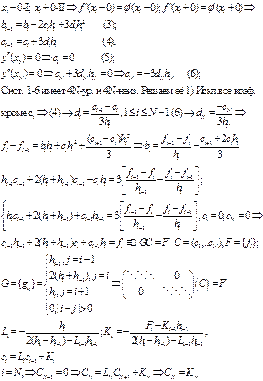
ЕДИНСТВЕННОСТЬ РЕШЕНИЯ КУБИЧЕСКОЙ ИНТЕРПОЛЯЦИИ

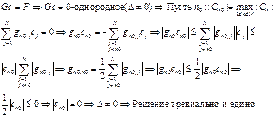
КВАДРАТНЫЕ СПЛАЙНЫ

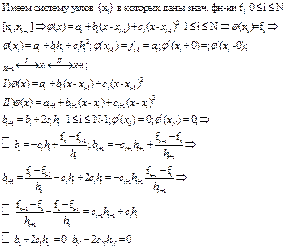
Оценим погрешность формулы (11), используя формулу Тейлора (по-прежнему предполагаем, что исходная функция обладает необходимым количеством производных):

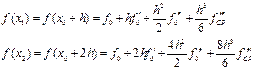
Подставляем эти выражения в правую часть (11). Тогда имеем:

Таким образом, согласно формуле (11) первая производная по трехточечной схеме имеет вид:

Произведем вычисления по формуле (12)

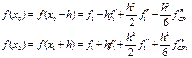Подстановка в правую часть (12) дает

и сравнение с правой частью приводит к следующему конечно-разностному выражению.

Из формул (13), (14) можем сделать несколько выводов. Во-первых, двучленные формулы первой производной (трехточечные схемы) имеют второй порядок точности. Справедлив более обший результат -нее двучленные формулы имеют второй порядок точности. Во-вторых, из сравнения (13) и (14) находим, что формула для центрально-разностной схемы вдвое точнее.

Чаще всего точная величина а неизвестна, и тогда вводят предельную абсолютную погрешность Δ_а, которую определяют как всякое число, не меньшее абсолютной погрешности

Погрешность результата арифметической операции с приближенными числами.

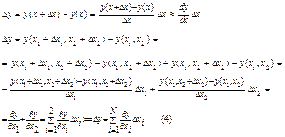
Т1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел.

Доказательство. Пусть  - приближенные числа. Рассмотрим алгебраическую сумму y = ±x₁±x₂±…±x_n (5)

Формулу (5) будем рассматривать как функцию n переменных. Очевидно, что. Используя (4), получим:

Δy = ±Δx₁ ± Δх₂ ±… ± Δх_n à |Δy| ≤ |Δx₁ |+ |Δх₂ |+… +| Δх_n|

Что и требовалось доказать.

Теорема Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.

Б13.

1.  Порядок аппроксимации производных на сетке

Одночленные формулы дифференцирования. Согласно одночленным формулам (7) и (8), первые две производные равны:

Вычисление первой производной проводится на отрезке [х₀, x₁], второй - на [х₀, x2]. Рассмотрим оценку точности вычислений основанную, на использовании ряда Тейлора (в общем случае формулы Тейлора) для представления исходной функции.