Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций, страница 2

Постановка задачи сплайновой интерполяции. Пусть есть сетка и в узлах задана исходная функция f _i. Задача метода заключается в том, чтобы построить интерполирующую функцию φ(х) в виде многочлена степени n так, что

1)  на каждом промежутке [X_i-1,X_i] функция φ(х) является многочленом степени n;

2) φ(х) совпадает с исходной функцией в узлах;

3) φ(х) имеет непрерывные производные до n - 1 порядка включительно.

Таким образом,

1) Сплайновая интерполяция является локальной, в отличие от глобальной лагранжевой, которая производится по всему промежутку определения функции.

2) степень многочлена и в сплайновой интерполяции может не совпадать с количеством отрезков интерполирования N-1.

3) вид лагранжева многочлена не зависит от порядка узлов, в то время как при сплайновой интерполяции узлы попарна упорядочены (явно указано, какой узел первый, а какой второй). 4) в лагранжевой интерполяции должны быть различны все узлы, в сплайновой - только соседние.

Линейная Сплайновая интерполяция.

В данном случае на каждом отрезке исходная функция аппроксимируется прямой линией. Очевидно, что графиком такой функции на всем промежутке [х₀, x_N ] будет ломаная прямая.

Пусть есть сетка , и в ее узлах заданы значения исходной функции f_i. На каждом отрезке [X_i-1,X_i ]построим интерполирующую функцию φ (х) так, чтобы последняя была линейна между соседними узлами и совпадала с исходной функцией в узлах:

Обратим внимание, что здесь индексация проводится по отрезкам, количество N которых и на 1 меньше, чем узлов. В узлах имеем равенства:

и эти равенства дают 2N соотношений для определения неизвестных констант а_i, и b_i

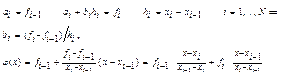
и в точности совпадает с интерполяционным многочленом Лагранжа в том случае, когда интерполяция проводится по двум точкам. Но в отличие от линейной лагранжевой интерполяции, с помощью сплайновой технологии можно аппроксимировать и неоднозначные кривые.

Интерполяция кубическими сплайнами

Если обозначить через у(х) отклонение от положения равновесия на каждом промежутке между узлами, то условием равновесия линейки является соотношение

Отсюда получаем, что кривая между соседними узлами имеет следующий вид: у(х) = А + Вх + Сх² +Dx³.y”(x0)=0,y”(N)=0

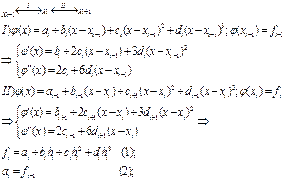
Б3.1. Погрешность интерполяции

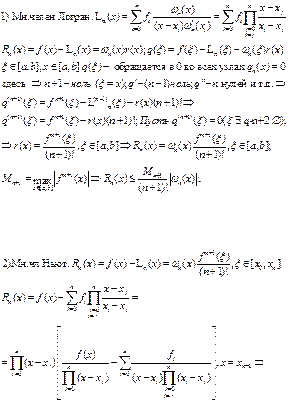
2 Формулы для приближения производных

Постановка задачи. Пусть есть упорядоченная сетка {х_n} x₀<x₁...<x_n ,на которой заданы значения функции {f_n}. Требуется определить значения производной в точках промежутка [х₀, х_n]. Основная идея численного дифференцирования функций заключается в том, чтобы дифференцировать интерполяционный многочлен φ(х) = L_n(x).  С учетом погрешности имеем следующее соотношение между исходной и интерполирующей функциями:

 Исходная формула это интерполяционный многочлен Ньютона:

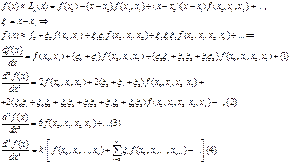 Для получения формул численного дифференцирования в выражениях (1) - (4) ограничиваются некоторым количеством слагаемых, при этом равенства для высших производных используются для оценки погрешности. Удержим в формулах

(1) - (4) по 2 в каждом выражении, причем первое будет давать формулу численного дифференцирования, а второе используем для оценки погрешности.

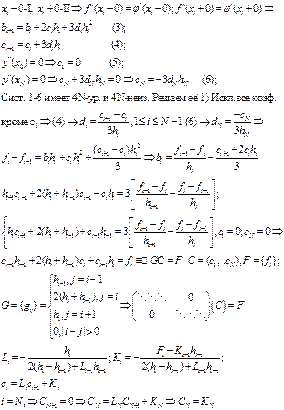
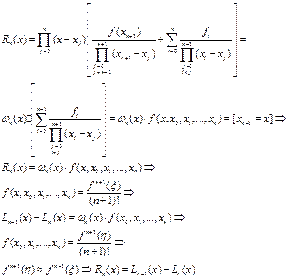Погрешности подразделяются на два вида: вычислительная погрешность (погрешность округления) и погрешность метода,. Рассмотрим влияние погрешности округления. Пусть в каждом узле f_i вычисляется с погрешностью ε_i т.е. реальная функция имеет вид (f_i + ε_i).Тогда вычислительная погрешность от такого неточного вычисления функции,:

 

Погрешность, связанная с неточным заданием функции, равна

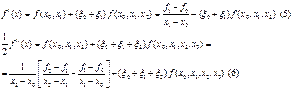Для оценки разделенной разности второго порядка, входящей в (5), используем главную часть формулы (6), а для разделенной разности третьего порядка используем (3). Тогда (5) и (6) примут вид: