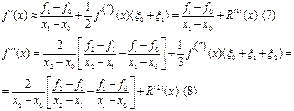Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций, страница 3

Подобные формулы, в которых в качестве главного члена используется первое слагаемое в (1) — (4), называются одночленными формулами. Оценим максимальную погрешность формул (7) - (8) на равномерной сетке, x_i+1-x_i=h = constТогда

линейная функция принимает наибольшее значение на одном из краев интервала.

Определение. Порядком точности приближенной формулы (например, формулы дифференцирования) называется число, равное показателю степени шага h старшего члена в погрешности этой формулы. Согласно этому определению, все одночленные формулы численного дифференцирования имеют первый порядок точности.

КВАДРАТНЫЕ СПЛАЙНЫ

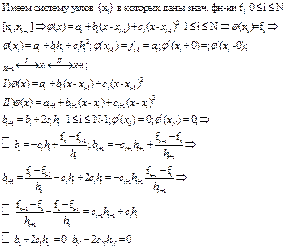
Аналогичным образом можно учесть и неточности вычисления аргументов. Эти погрешности обязательно нужно учитывать, но они не носят принципиального характера. Что касается погрешности метода, то для нее мы имеем основную оценку

Зависимость от количества узлов содержится в (n+1)! и в функции ω(х).  Обратная интерполяция При построении многочлена Лагранжа в качестве сетки выбиралась упорядоченную последовательность узлов, причем друг от друга они располагаются на произвольных расстояниях. каждому значению аргумента должно соответствовать одно значение функции. Поэтому лагранжева интерполяция используется только для однозначных функций и неприменима для многозначных функций. Задачей обратного интерполирования является нахождение зависимости x(f) по заданной таблице

f_t = f(x_i). Для этого необходима однозначность обратной функции. Такая задача разрешима, если исходная функция монотонна, либо интерполяция производится на отрезках монотонности исходной функции. Важным приложением этой задачи является решение алгебраических или трансцендентных уравнений f(x) = 0 . Для этого строится обратный интерполяционный многочлен

Простейшие формулы численного дифференцирования на равномерной сетке. Вычисление погрешности с помощью представления функции по формуле Тейлора.

Одночленные формулы дифференцирования. Согласно одночленным формулам (7) и (8), первые две производные равны:

Вычисление первой производной проводится на отрезке [х₀, x₁], второй - на [х₀, x2]. Рассмотрим оценку точности вычислений основанную, на использовании ряда Тейлора (в общем случае формулы Тейлора) для представления исходной функции.

Рассмотрим вначале формулу первой производной (9) и оценим ее погрешность в узлах х₀ и x₁. Для этого используем следующий прием: произведем разложение главного слагаемого правой части (9) по формуле Тейлора в узле х₀, и сравним результат с левой частью:

Подставляя f1в правую часть (9), имеем:

Вычитая это выражение из левой части (9), получаем:

простейшая одночленная формула для первой производной является формулой первого порядка точности.

Рассмотрим теперь формулу второй производной (10). представим первое слагаемое правой части в виде разложения по формулу Тейлора в координате одного из узлов. Рассмотрим производную в окрестности точки х₀, левой точки промежутка

[х₀, x₂]. Для этого нужно разложить f₁; и f₂  B окрестности точки х₀

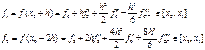
Как и в случае формулы (9) мы предполагаем, что исходная функция обладает необходимым количеством производных для представления ее по формуле Тейлора. Тогда имеем

одночленная формула второй производной тоже является формулой первого порядка точности. Определим теперь погрешность в среднем узле промежутка х₁. Для этого нужно разложить f₀ и  f₂в окрестности этой точки:

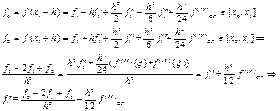
в средней точке промежутка погрешность оказалась пропорциональной не первой степени h, а квадрату шага h²-второй порядок точности формулы (10) в средней точке интервала.

Двучленные формулы численного дифференцирования для получения формул численного дифференцирования используем первые два слагаемых.

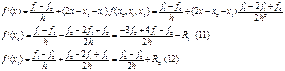
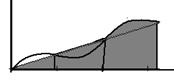
Формула трапеций