Рассмотрим вначале формулу первой производной (9) и оценим ее погрешность в узлах х0 и x1. Для этого используем следующий прием: произведем разложение главного слагаемого правой части (9) по формуле Тейлора в узле х0, и сравним результат с левой частью:
![]()
Подставляя fiв правую
часть (9), имеем: ![]()
Вычитая это выражение из левой части (9), получаем:
![]() простейшая одночленная формула для первой производной
является формулой первого порядка точности.
простейшая одночленная формула для первой производной
является формулой первого порядка точности.
Рассмотрим теперь формулу второй производной (10). представим первое слагаемое правой части в виде разложения по формулу Тейлора в координате одного из узлов. Рассмотрим производную в окрестности точки х0, левой точки промежутка
[х0, x2]. Для этого нужно разложить f1; и f2 B окрестности точки х0
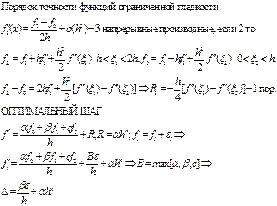
Доказательство.
Пусть ![]() à
à
![]()
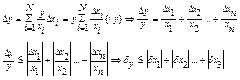
Теорема. Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.
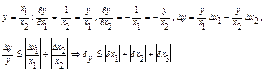
Первый, заключается в отбрасывании знаков числа, количество которых превышает количество разрядов п, с которым работает машина. Если мы хотим удержать в числе первые п знаков, и в следующем (n +1) разряде стоит цифра аn+1 > 5, то к п разряду добавляется единица. В противном случае цифра n -го порядка остается без изменений.
Определение. Первые n значащих цифр (знаков) верные, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого п- значащей цифрой. Это означает, что если известно, что в записи числа
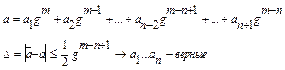
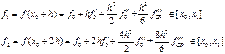
Как и в случае формулы (9) мы предполагаем, что исходная функция обладает необходимым количеством производных для представления ее по формуле Тейлора. Тогда имеем
![]() одночленная формула второй производной тоже является
формулой первого порядка точности. Определим теперь погрешность в среднем
узле промежутка х1. Для этого нужно разложить f0 и f2в окрестности этой точки:
одночленная формула второй производной тоже является
формулой первого порядка точности. Определим теперь погрешность в среднем
узле промежутка х1. Для этого нужно разложить f0 и f2в окрестности этой точки:
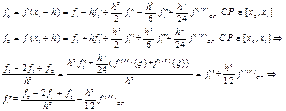 в
средней точке промежутка погрешность оказалась пропорциональной не первой
степени h, а квадрату шага h2-второй
порядок точности формулы (10) в средней точке интервала.
в
средней точке промежутка погрешность оказалась пропорциональной не первой
степени h, а квадрату шага h2-второй
порядок точности формулы (10) в средней точке интервала.
Двучленные формулы численного дифференцирования для получения формул численного дифференцирования используем первые два слагаемых.
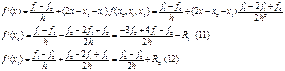
Б14.
1. Числа рациональные и иррациональные, представление чисел в компьютере, ошибки округления
Определение. Число - это определенным образом упорядоченная последовательность цифр. Действительное число единственным образом представляется в виде бесконечной суммы
![]()
Здесь ai - цифры, аn ≠ 0, n — целое. Число g > 0 называется основанием системы счисления. При этом 0≤ai≤g-1à
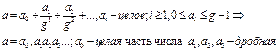 Определение.
Если в дробной части формулы (3) последовательность цифр начиная с ак
является повторяющейся, т.е.
Определение.
Если в дробной части формулы (3) последовательность цифр начиная с ак
является повторяющейся, т.е.
![]() то
такое число называется рациональным. Рациональное число может быть
представлено в виде
то
такое число называется рациональным. Рациональное число может быть
представлено в виде ![]()
Если в бесконечной последовательности нет периодически повторяющейся последовательности, то число иррационально. Замечание. Все системы счисления используют для записи чисел некоторое количество цифр, по крайней мере, цифры 0 и 1 содержат все системы. Поэтому, до тех пор, пока не указана система счисления, не определено и значение числа.
Определение. Погрешностью определения (записи) числа а является
разность между приближенным значением а и точной величиной а:![]() .
.
Определение. Абсолютной погрешностью числа а называется модуль Δa ![]()
Определение. Относительная погрешность есть отношение абсолютной
погрешности к модулю числа ![]()
2. Метод простой итерации решения системы линейных уравнений. Условие сходимости.
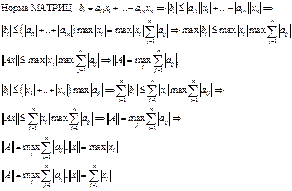 МЕТОД
ПРОСТОЙ ИТТЕРАЦИИ
МЕТОД
ПРОСТОЙ ИТТЕРАЦИИ
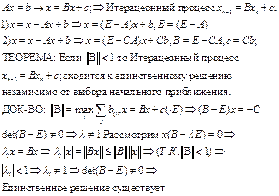
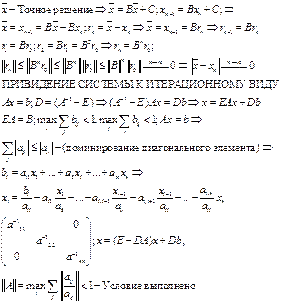
2. Порядок аппроксимации схемы для ОДУ 2 порядка
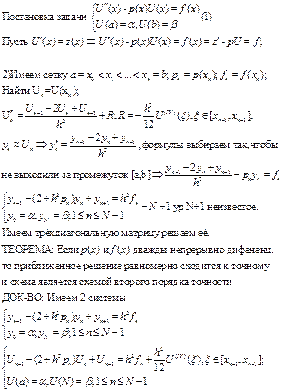
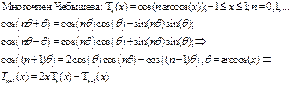
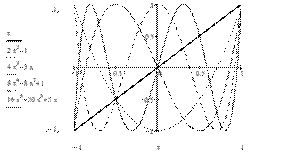
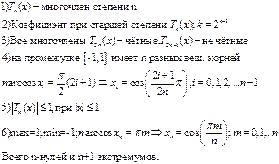
Б15.
1. Метод Ньютона для отыскания корней
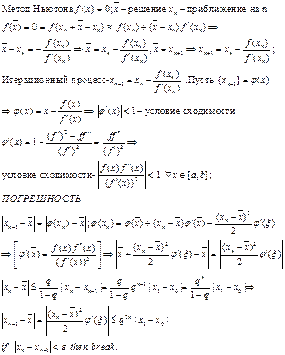
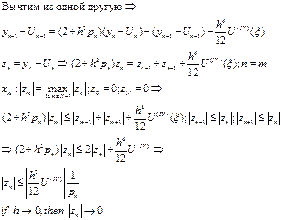
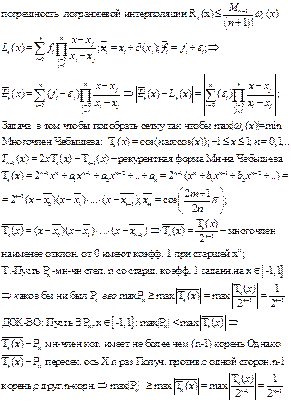
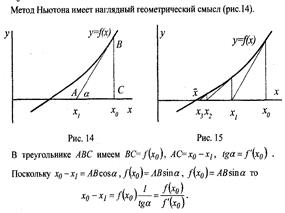
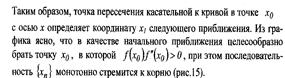
2. Норма в пространстве непрерывных функций. Многочлены наименее уклоняющиеся от нуля
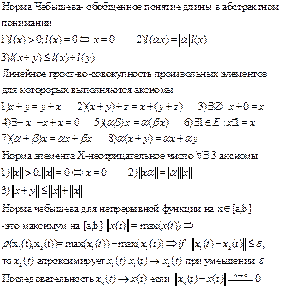
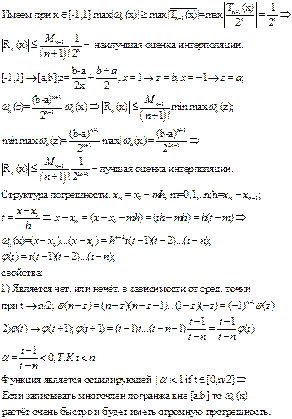
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.