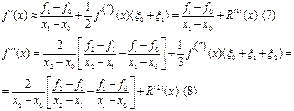Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций, страница 5

Подобные формулы, в которых в качестве главного члена используется первое слагаемое в (1) — (4), называются одночленными формулами. Оценим максимальную погрешность формул (7) - (8) на равномерной сетке, x_i+1-x_i=h = constТогда

линейная функция принимает наибольшее значение на одном из краев интервала.

Определение. Порядком точности приближенной формулы (например, формулы дифференцирования) называется число, равное показателю степени шага h старшего члена в погрешности этой формулы. Согласно этому определению, все одночленные формулы численного дифференцирования имеют первый порядок точности.

Оценим погрешность формулы (11), используя формулу Тейлора (по-прежнему предполагаем, что исходная функция обладает необходимым количеством производных):

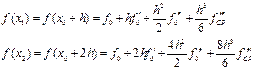
Подставляем эти выражения в правую часть (11). Тогда имеем:

Таким образом, согласно формуле (11) первая производная по трехточечной схеме имеет вид:

Произведем вычисления по формуле (12)

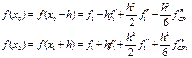Подстановка в правую часть (12) дает

и сравнение с правой частью приводит к следующему конечно-разностному выражению.

Из формул (13), (14) можем сделать несколько выводов. Во-первых, двучленные формулы первой производной (трехточечные схемы) имеют второй порядок точности. Справедлив более обший результат -нее двучленные формулы имеют второй порядок точности. Во-вторых, из сравнения (13) и (14) находим, что формула для центрально-разностной схемы вдвое точнее.

2. Сплайны

Постановка задачи сплайновой интерполяции. Пусть есть сетка и в узлах задана исходная функция f _i. Задача метода заключается в том, чтобы построить интерполирующую функцию φ(х) в виде многочлена степени n так, что

1)  на каждом промежутке [X_i-1,X_i] функция φ(х) является многочленом степени n;

2) φ(х) совпадает с исходной функцией в узлах;

3) φ(х) имеет непрерывные производные до n - 1 порядка включительно.

Таким образом,

1) Сплайновая интерполяция является локальной, в отличие от глобальной лагранжевой, которая производится по всему промежутку определения функции.

2) степень многочлена и в сплайновой интерполяции может не совпадать с количеством отрезков интерполирования N-1.

3) вид лагранжева многочлена не зависит от порядка узлов, в то время как при сплайновой интерполяции узлы попарна упорядочены (явно указано, какой узел первый, а какой второй). 4) в лагранжевой интерполяции должны быть различны все узлы, в сплайновой - только соседние.

Линейная Сплайновая интерполяция.

В данном случае на каждом отрезке исходная функция аппроксимируется прямой линией. Очевидно, что графиком такой функции на всем промежутке [х₀, x_N ] будет ломаная прямая.

Пусть есть сетка , и в ее узлах заданы значения исходной функции f_i. На каждом отрезке [X_i-1,X_i ]построим интерполирующую функцию φ (х) так, чтобы последняя была линейна между соседними узлами и совпадала с исходной функцией в узлах:

Обратим внимание, что здесь индексация проводится по отрезкам, количество N которых и на 1 меньше, чем узлов. В узлах имеем равенства:

Простейшие формулы численного дифференцирования на равномерной сетке. Вычисление погрешности с помощью представления функции по формуле Тейлора.

Одночленные формулы дифференцирования. Согласно одночленным формулам (7) и (8), первые две производные равны:

Вычисление первой производной проводится на отрезке [х₀, x₁], второй - на [х₀, x2]. Рассмотрим оценку точности вычислений основанную, на использовании ряда Тейлора (в общем случае формулы Тейлора) для представления исходной функции.

Рассмотрим вначале формулу первой производной (9) и оценим ее погрешность в узлах х₀ и x₁. Для этого используем следующий прием: произведем разложение главного слагаемого правой части (9) по формуле Тейлора в узле х₀, и сравним результат с левой частью:

Подставляя fiв правую часть (9), имеем:

Вычитая это выражение из левой части (9), получаем: