Интерполяция многочленами. Числа, представление чисел, рациональные и иррациональные числа. Сплайны, простейшие сплайны, построение сплайна. Сходимость схемы Эйлера. Норма в пространстве непрерывных функций, страница 4

Оценим погрешность формулы (11), используя формулу Тейлора (по-прежнему предполагаем, что исходная функция обладает необходимым количеством производных):

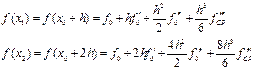
Подставляем эти выражения в правую часть (11). Тогда имеем:

Таким образом, согласно формуле (11) первая производная по трехточечной схеме имеет вид:

Произведем вычисления по формуле (12)

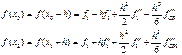Подстановка в правую часть (12) дает

и сравнение с правой частью приводит к следующему конечно-разностному выражению.

Из формул (13), (14) можем сделать несколько выводов. Во-первых, двучленные формулы первой производной (трехточечные схемы) имеют второй порядок точности. Справедлив более обший результат -нее двучленные формулы имеют второй порядок точности. Во-вторых, из сравнения (13) и (14) находим, что формула для центрально-разностной схемы вдвое точнее.

2. Формулы численного интегрирования

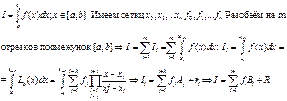Формулы прямоугольников

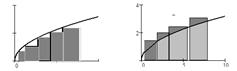
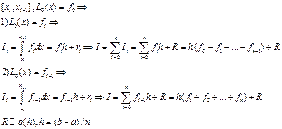
Формула Симпсона

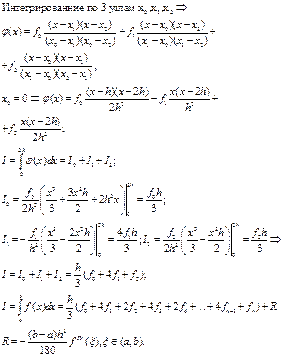
Б4.

1. Численное решение ОДУ 1 порядка. Схема Эйлера

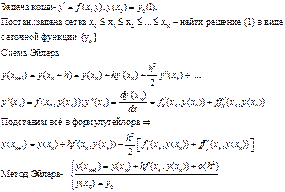
Геометрический смысл-Δy=f(x₀y₀)Δx  Δy=y’́Δx=tg(ά)́Δx

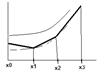
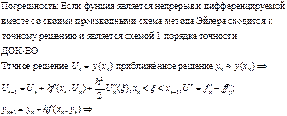
Формула средних

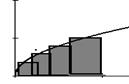
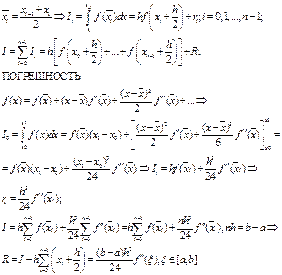
Б5.

1. Многочлены Чебышева Рекуррентная формула

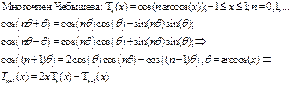
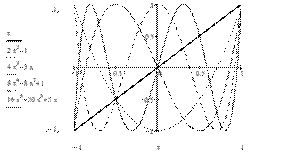
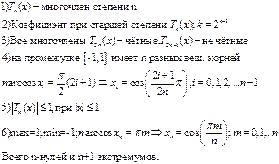
2. Численное интегрирование (методы прямоугольников и трапеций)

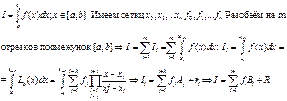Формулы прямоугольников

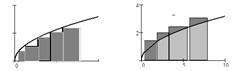
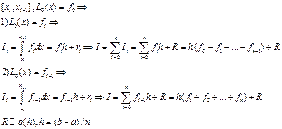
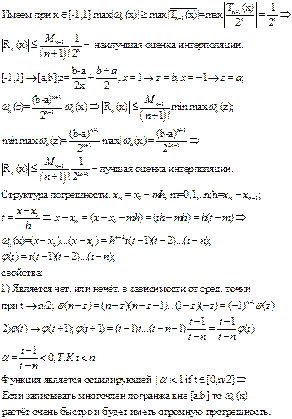
Б8.

1. Сходимость схемы Эйлера

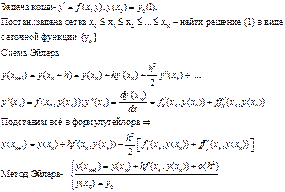
Геометрический смысл-Δy=f(x₀y₀)Δx  Δy=y’́Δx=tg(ά)́Δx

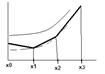
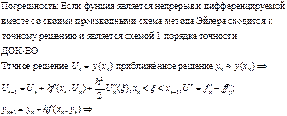
Формула трапеций

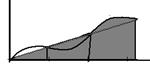
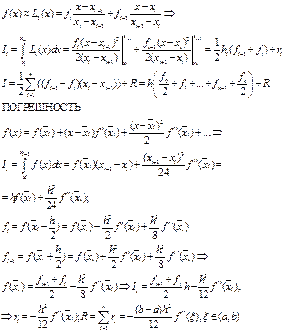
2. Краевая задача для ОДУ 2 порядка и разностная схема для нее

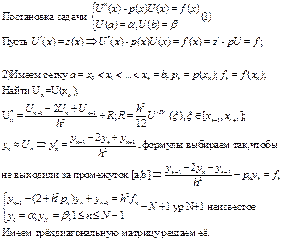
МЕТОД ПРОГОНКИ

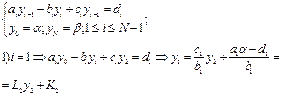
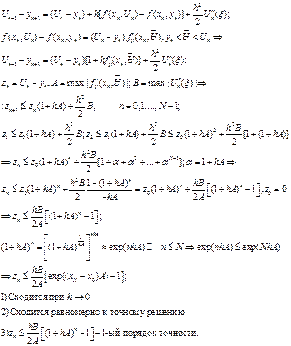
 Б6.

1. Оптимальное расположение узлов интерполяции. Многочлены наименее уклоняющиеся от нуля.

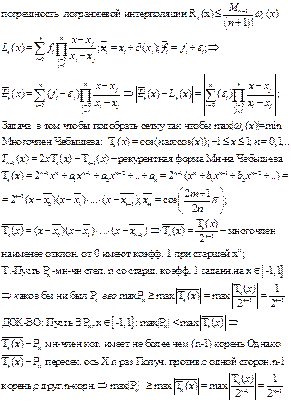
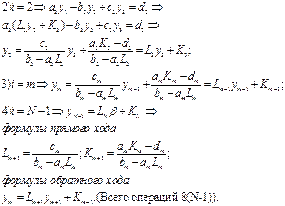
Единственность решения

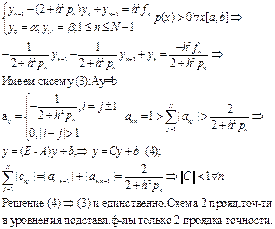
2. Метод Монте-Карло

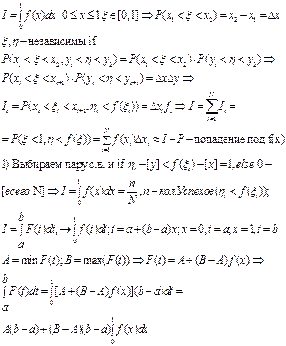
Второй способ вычисления, заключается в том, что интеграл рассматривается как математическое ожидание от случайной функции f с равномерной плотностью распределения от равномерно распределенной величины х.

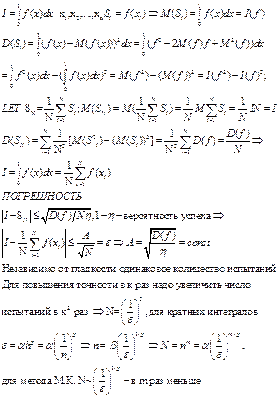
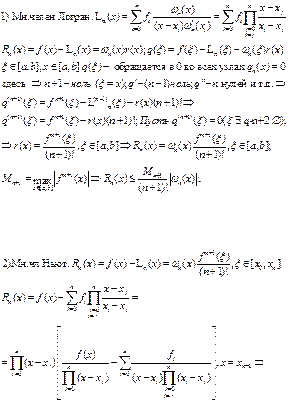
Б7.

1. Порядок аппроксимации и сходимость разностной схемы. Порядок аппроксимации разностной схемы Эйлера

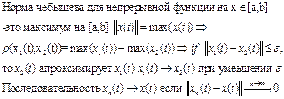
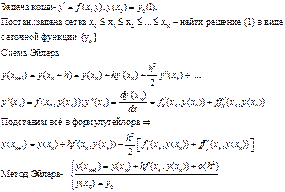
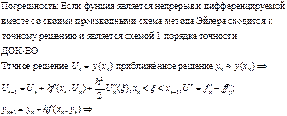
Б9.

1. Интерполяционный многочлен Лагранжа

Интерполяционный многочлен логранжа

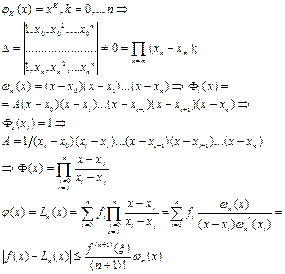
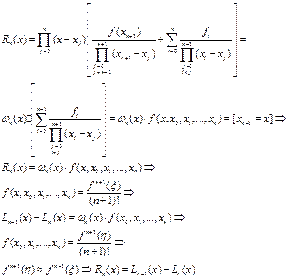
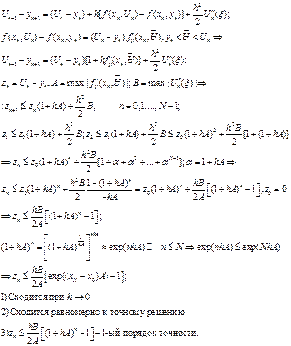
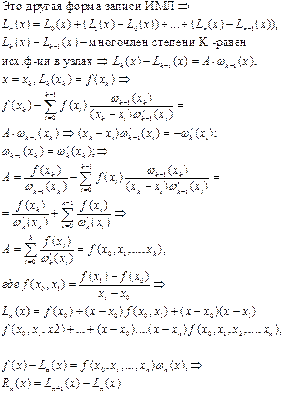
2. Метод прогонки

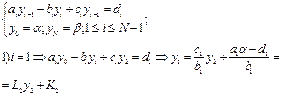
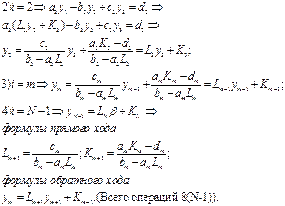
2. Достаточное условие применимости метода Гаусса

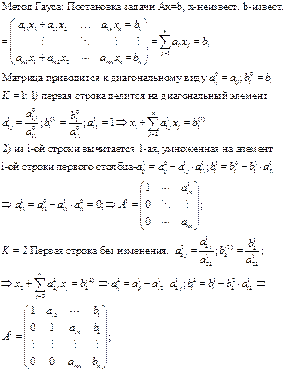
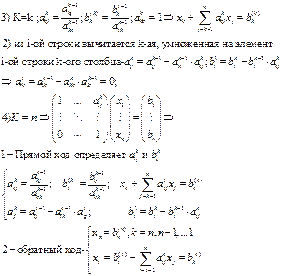
СХЕМА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА

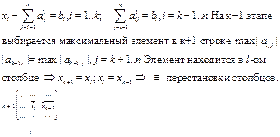
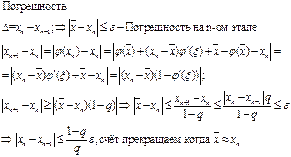ГЕОМЕТРИЧЕСКИЙ СМЫСЛ x=φ(x).

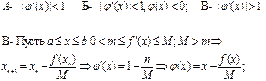
Б11.

1.  Метод деления отрезка пополам для отыскания корней

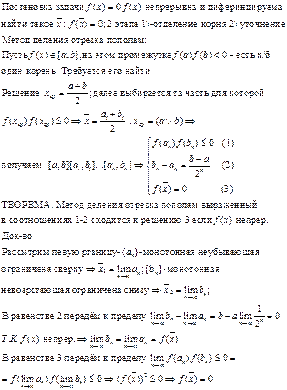
МЕТОД ХОЛЕЦКОГО

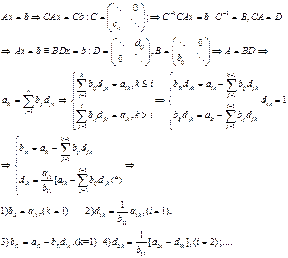ДОСТАТОЧНЫЙ ПРИЗНАК РАЗРЕШИМОСТИ

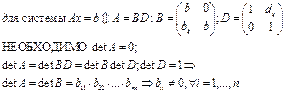
2. Метод Гаусса с выбором главного элемента

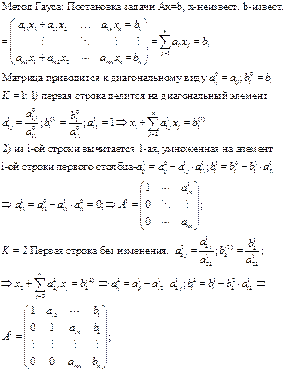
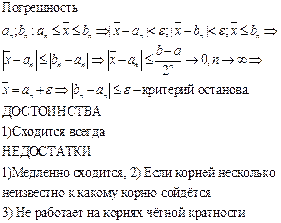
Б10. 1. Сходимость метода простой итерации для отыскания корней уравнений

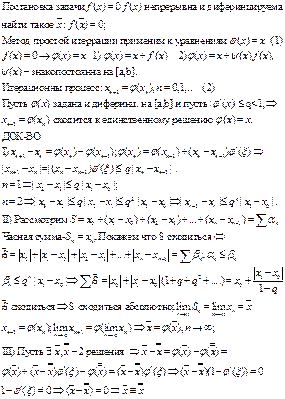
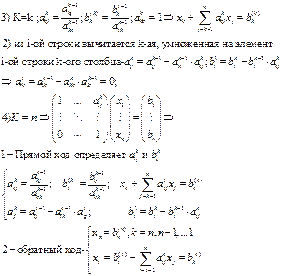
СХЕМА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА

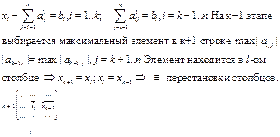
2. Приближенное дифференцирование

Постановка задачи. Пусть есть упорядоченная сетка {х_n} x₀<x₁...<x_n ,на которой заданы значения функции {f_n}. Требуется определить значения производной в точках промежутка [х₀, х_n]. Основная идея численного дифференцирования функций заключается в том, чтобы дифференцировать интерполяционный многочлен φ(х) = L_n(x).  С учетом погрешности имеем следующее соотношение между исходной и интерполирующей функциями:

 Исходная формула это интерполяционный многочлен Ньютона:

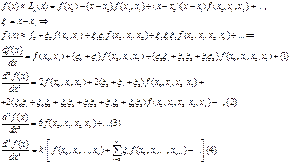 Для получения формул численного дифференцирования в выражениях (1) - (4) ограничиваются некоторым количеством слагаемых, при этом равенства для высших производных используются для оценки погрешности. Удержим в формулах

(1) - (4) по 2 в каждом выражении, причем первое будет давать формулу численного дифференцирования, а второе используем для оценки погрешности.

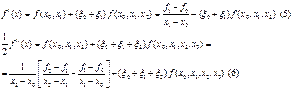Для оценки разделенной разности второго порядка, входящей в (5), используем главную часть формулы (6), а для разделенной разности третьего порядка используем (3). Тогда (5) и (6) примут вид: