Мартенситные превращения. Мартенситное превращение в сплавах на основе железа. Строение мартенсита в сплавах с цветными и благородными металлами, страница 8

Из анализа рельефа на поверхности предварительно полированного шлифа в месте образования нового кристалла можно определить характер макроскопической деформации, которая является результатом смещений атомов или деформации решетки в макроскопическом объеме. Такое исследование было проведено Гренингером и Трояно (1949 г.) на образцах сплава Fe - 22 мас. % Ni - 0,8 мас. % С, в которых превращение аустенита в мартенсит происходило только при охлаждении ниже комнатной температуры. Установлено, что поверхность превращенной области материала наклоняется к плоскости шлифа, но остается плоской (рисунок 112); прямые риски, проведенные на поверхности шлифа до превращения, в результате образования кристалла мартенсита претерпевают излом на выходе поверхности габитуса и меняют свое направление, но остаются прямыми; в целом сохраняется непрерывность этих линий. Это свидетельствует о том, что рельеф является результатом однородной деформации с инвариантной плоскостью, т. е. имеется плоскость (плоскость габитуса кристалла мартенсита), которая не искажается и не поворачивается; все смещения материала направлены в одну сторону и пропорциональны расстоянию от инвариантной плоскости.

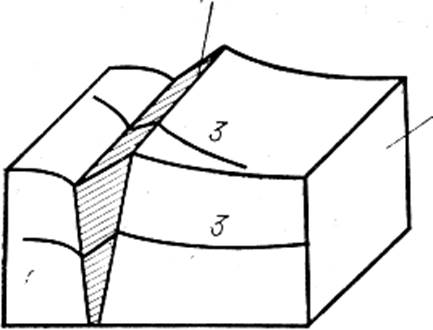
1 – исходная фаза; 2 – новая фаза (мартенсит); 3 – линия, проведенная на плоской поверхности образца, в исходном состоянии она остается непрерывной и после образования мартенситной фазы

Рисунок 112 – Характер рельефа, возникающего на поверхности полированного шлифа в результате образования кристалла мартенсита

Примером деформации с инвариантной плоскостью может служить одноосное растяжение или сжатие (вектор смещения перпендикулярен к инвариантной плоскости) или сдвиг (вектор смещения параллелен инвариантной плоскости); любую деформацию с инвариантной плоскостью можно представить комбинацией этих двух простых деформаций. Все смещения при деформации с инвариантной плоскостью происходят в одной плоскости, в которой лежат нормаль к инвариантной плоскости и вектор смещения; таким образом, деформация оказывается плоской. Следует отметить, что не всякая плоская однородная деформация происходит при наличии инвариантной плоскости.

В этом легко убедиться, рассматривая деформацию сферического объема кристалла (рисунок 113). Однородная деформация превращает этот объем в эллипсоид. Деформация с инвариантной плоскостью имеет место, если по одной из главных осей нет деформации (например, по оси x₁, λ₁=1),а по двум другим главным осям деформации различны по знаку: по одной (например, по оси x₂) деформация λ₂>1, а по другой (x₃) деформация λ₃<1 (см. рисунок 113а). Если и одновременно больше или меньше 1, эллипсоид не пересекает исходную сферу (см. рисунок 113б), так что ни одно из плоских сечений эллипса не сохраняет длины исходного диаметра; при λ₁=1 происходит только касание сферы и эллипсоида вдоль одной линии (оси x₁). При условии λ₂>1, λ₃<1 (или, наоборот, λ₂<1, λ₃>1) легко найти плоское сечение, которое сохраняется инвариантным.

а

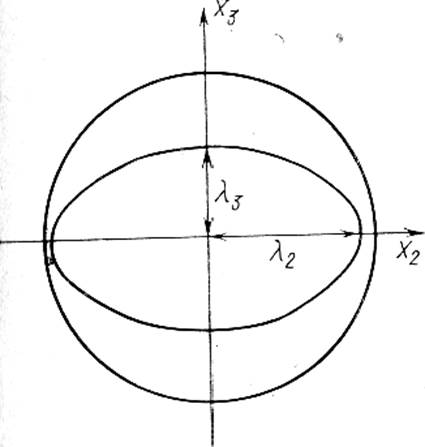
б

Рисунок 113 – Плоская деформация сферического объёма кристалла с инвариантной плоскостью (а) и без нее (б)

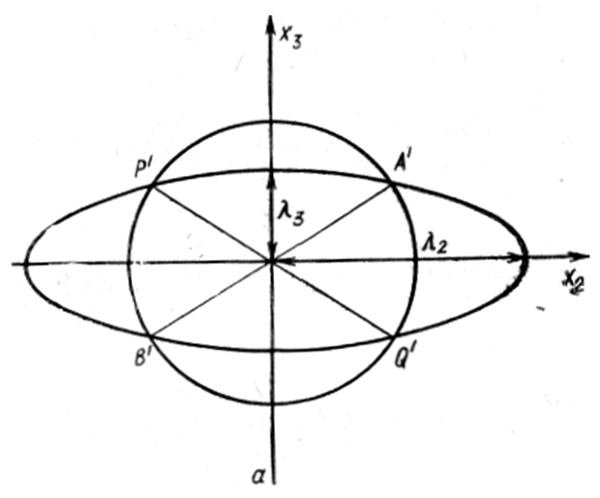
Рисунок 114 – Определение инвариантной плоскости сферического объема и эллипсоида деформации (а) и взаимного эллипсоида деформации (б)

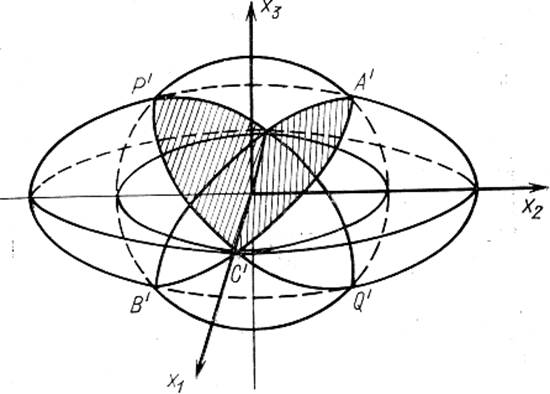
На рисунке 114а показаны сечения исходной сферы и эллипсоида деформации в координатной плоскости х₂х₃. Пересечения окружности и эллипса в точках А и В, Р и Q означают сохранения длины исходного диаметра. Поскольку λ₁=1, то не меняет своей длины и диаметр по оси x₁. Плоскость проведённая через диаметр А'В' (или P'Q') и ось х₁, остается неискаженной, все линии в этой плоскости не изменяют своей длины при деформации, хотя она может поворачиваться.

Для определения положения инвариантной плоскости до деформации необходимо построить так называемый взаимный эллипсоид, т. е. выделить в кристалле такой эллипсоид, который в результате деформации превратился бы в сферу единичного радиуса (см. рисунке 114б). Пересечение этой сферы и взаимного эллипсоида дает положение инвариантной плоскости до деформации (сечения АВ и PQ на рисунке 114б).