(001)γ ║ (001)α (266)
[100]γ ║ [110]α. (267)
Такое ориентационное соотношение известно как соотношение Бейна. Оно наблюдалось при превращении в очень тонких пленках.
Мартенситные пластины в обычных (массивных) образцах стали с содержанием 0,5-1,4 мас.%С находятся в следующем ориентационном соотношении с аустенитом:
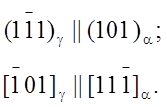 (268)
(268)
Это соотношение известно как соотношение Курдюмова-3акса. В сплаве Fe - 30 мас. °/о Ni установлено соотношение вида
(111)γ ║ (101)α; (269)
[112]γ ║ [101]α(270)
Это соотношение, известно как соотношение Нишиямы, так же как и соотношение (268), связано с деформацией Бейна (см. рисунок 121) и отличается от соотношения Курдюмова - Закса не очень сильно: например, угол между направлениями [101]α составляет около 5˚ (рисунок 122). Кроме указанных соотношений известно соотношение Гренинга и Трояно (найдено в сплаве Fe – 22 мас.% Ni – 0,8 мас.% С). Это промежуточное соотношение между (266), (267) и (268) и не выделяет каких-либо других совпадающих рациональных кристаллографических направлений в тех же сопрягающихся плоскостях (111)γ и (101)α. Кроме перечисленных ориентационных соотношений, следующих из схемы Бейна или по крайней мере не противоречащих ей существует еще один весомый аргумент в пользу реальности этой схемы деформации решетки. Тетрагональность решетки мартенсита углеродсодержащей стали объясняется упорядоченным расположением атомов углерода в одной из трех подсистем октаэдрических позиций решетки α-железа: вдоль оси [001]. Как видно из рисунка 121, деформация Бейна автоматически переводит все октаэдрические поры г.ц.к. решетки аустенита в одну подсистему октаэдрических пор о.ц.к. решетки мартенсита.
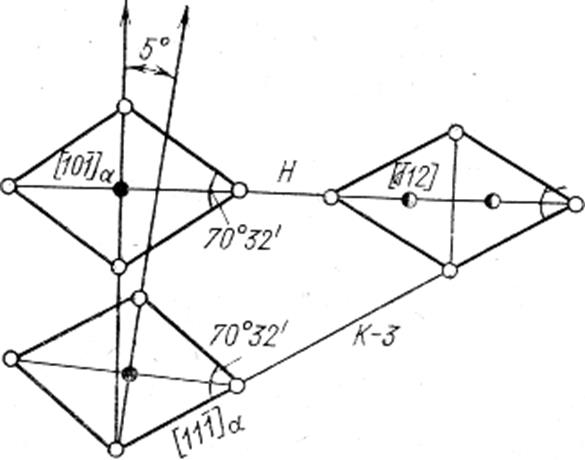
Рисунок 122 – Ориентационные соотношения
Бейна, Курдюмова – Закса и Нишиямы
Убедившись в реальности деформации Бейна, следует поискать дополнительную к ней деформацию, которая приведет к известному из эксперимента ориентационному соотношению.
Из рисунка 123 видно, что для сохранения первоначальной ориентации плоскости (111)γ после ее превращения в результате бейновской деформации в плоскость (101)α необходимо вращение вокруг направления [110]γ. Такая сложная деформация приведет к реализации соотношения Нишиямы. Эту деформацию можно записать как произведение матриц
Dн = R[110]γDБ (271)
Наиболее простой вид полная деформация решётки приобретает, если вместо обычных координатных осей решетки аустенита взять систему (ортогональных) осей [-112]γ, [-1-11]γ, [110]γ:
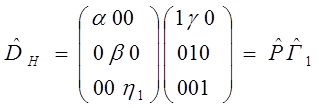 (272)
(272)
Выражение (272) показывает, что полная деформация решетки может быть представлена как простой сдвиг Г1, вдоль [-112]γ по плоскости (1–11)γ с последующим изменением размеров вдоль выбранных координатных осей (Р).
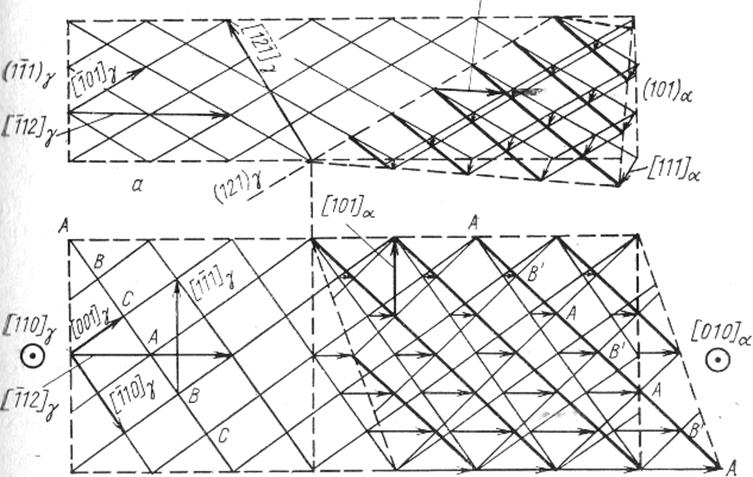
Рисунок 123 – Деформация решетки при перестройке решетки
г.ц.к®о.ц.к
Как видно из рисунка 123б сдвиг Г1 приводит к замене чередования плотноупакованных плоскостей типа АВСА, характерного для г.ц.к. решетки на чередование типа АВ'А, характерное для о.ц.к. решетки в последовательности плоскостей {110}. Сдвиг каждой плоскости (111) относительно рядом расположенной происходит на 1/12 а [-1 1 2] поскольку эти плоскости отстоят друг от друга на расстояние 1/3а [-1 1 1], то величина сдвига γ=1/12 а [-1 1 2]/1/3 а[ 1 1 -1]= √2/4=0,35.
Деформация Р относится к изменению межплоскостного расстояния dэлемент матрицы (β) и к изменению расположения атомов в плотноупакованных слоях путем растяжения вдоль [112] и сжатия по [110]r (для сплава Fe – 30% Ni α= + 13 %, ηı = -7,5%, β близка к нулю).
Из приведенного анализа, исходными данными для которого были только представления о чистой (т. е. без вращения) деформации решетки по Бейну и экспериментальная характеристика конечного состояния – ориентационное соотношение, следует, что:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.