Мартенситные превращения. Мартенситное превращение в сплавах на основе железа. Строение мартенсита в сплавах с цветными и благородными металлами, страница 10

Однородная деформация в случае, когда ни одно из значений λ≠1 (объемный случай) не дает инвариантной плоскости, но сохраняет инвариантность линий вдоль образующих конуса (рисунок 116). 3адача теоретического анализа состоит в том, чтобы при известных параметрах исходной и образующейся фаз, а следовательно, при заданной чистой деформации решетки выбрать дополнительную деформацию, не меняющую решетку (сдвиг, двойникование), которая давала бы в сумме с заданной деформацией решетки результирующую плоскую деформацию с инвариантной плоскостью. Дополнительный сдвиг должен для этого удовлетворять следующим условиям: 1) плоскость сдвига Р должна пересекать конус инвариантных направлений; 2) плоскость, перпендикулярная к вектору направления сдвига 1, также должна пересекать конус инвариантных направлений.

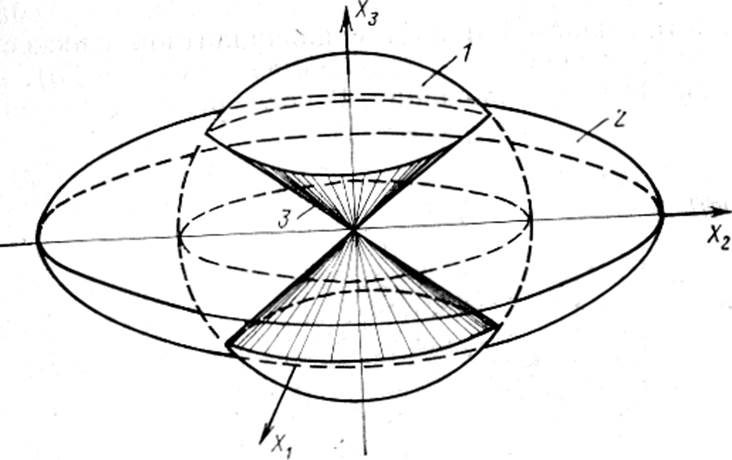
1 – единичная сфера в исходной решетке; 2 – эллипсоид деформации;

3 – конус инвариантных линий

Рисунок 116 – Деформация решетки (объемный случай)

Выбор деформации решетки для описания превращений. Примеры превращений, осуществляемых деформацией решетки без дополнительной деформации. Кооперативный характер перестройки решетки состоит в согласованном движении атомов, когда атомы не обмениваются местами, а лишь смещаются относительно своих соседей на расстояния, не превышающие межатомных. При этом, хотя каждый атом по отношению к своему соседу смещается на расстояние меньше межатомного, смещение атома, отстоящего от места начала роста кристалла новой фазы, на макроскопическую величину, будет также макроскопическим. Если вектор смещения (сдвига) равен полной трансляции решетки, то в результате любого числа таких смещений кристаллическая структура не изменится. Примером таких смещений является пластическая деформация, осуществляемая при движении полных дислокаций (деформация при инвариантной решетке). Хорошо известным примером кооперативного процесса перемещения атомов приводящего к перестройке кристаллической решетки, является механическое двойникование. Чтобы описать результат фазового превращения как деформацию решетки, необходимо принять условие соответствия всех узлов исходной решетки и решетки новой фазы. Это условие связывает положения узлов элементарных ячеек решеток новой и исходной фаз, которые выбирают так, чтобы они содержали одинаковое число атомов. В случае однородной деформации решетки должны быть выбраны главные оси и значения главных деформаций для перехода исходной решетки в новую. Выбор условий соответствия, эквивалентных по числу узлов ячеек, и, следовательно, величин деформаций может иметь много вариантов (рисунок 117).

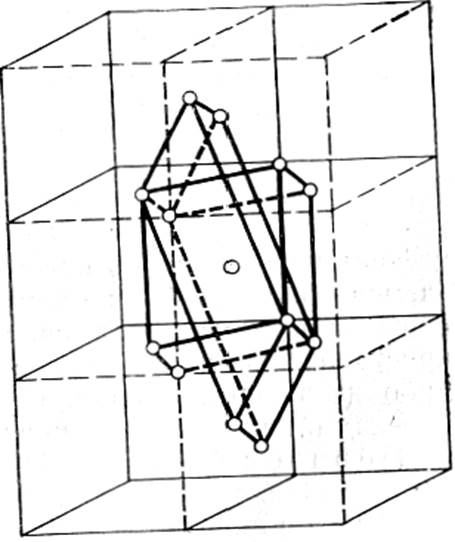
Рисунок 117 – Многозначность выбора деформации решетки

Очевидно, наиболее реальным является предположение, что атом узла исходной решетки занимает ближайший к нему узел новой решетки, т. е. деформация выбирается минимальной. Условие деформации решетки с инвариантной плоскостью (без какой-либо дополнительной деформации) выполняется лишь в исключительных случаях. Деформация решетки является плоской и идет с инвариантной плоскостью при превращении г.п.у.↔г.ц.к. (например, α-Со↔β-Со), а также при механическом двойниковании. В последнем случае определить деформацию решетки очень просто, поскольку форма и размер элементарной ячейки не изменяется.

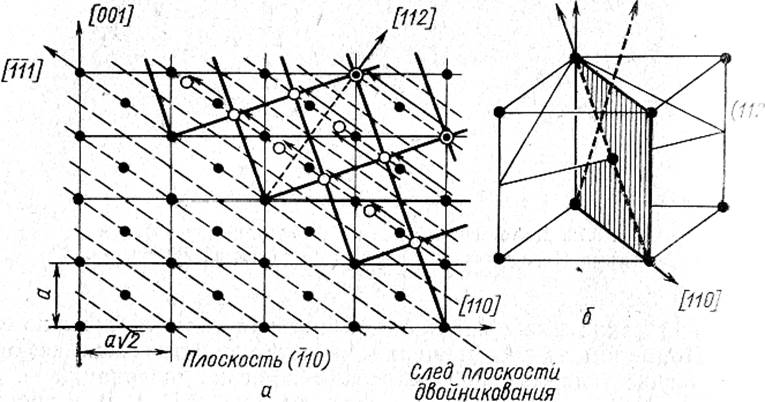
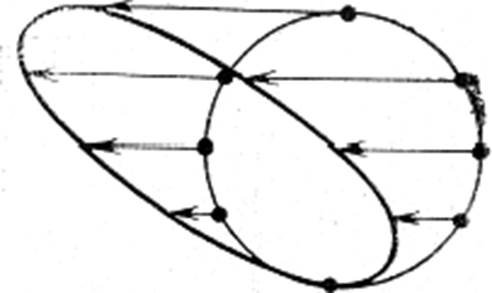
Рисунок 118 – Двойникование в о.ц.к. решётки

В обоих случаях деформации решетки представляют собой простой сдвиг, матрица и новый кристалл сохраняют когерентность по границе раздела без каких-либо искажений. Граница раздела фаз (поверхность габитуса) плоская и параллельная инвариантной плоскости.

Образование двойника в о.ц.к. кристалле. Процесс двойникования можно рассматривать как превращение не связанное с действием химической движущей силы. 3десь этот процесс рассматривается как наглядный пример кооперативного движения атомов. В свою очередь, мартенситное превращение, поскольку оно сопровождается изменением формы превращенного объема, может быть своеобразным механизмом пластической деформации в сплавах определенного типа. Образование мартенсита во время пластической деформации дает эффект чрезвычайно высокой пластичности и одновременно приводит к упрочнению.