Имеются и другие превращения, в которых диффузия, несомненно, контролирует процесс, но который соответствует оси геометрии мартенситного превращения. Например, выделение фазы Cu-Be из α–твердого раствора и упорядочение фазы Cu-Au. Существуют и другие реакции выделения, имеющие типичные мартенситные черты. Становится все более трудно дифференцировать превращения с зародышем и ростом при рассмотрении ряда особых случаев, если не принимать за критерий изменение формы при превращении.
Механизмы роста кристаллов при бездиффузионных превращениях.
Если скорость превращения определяется скоростью перемещения границы раздела фаз, различающихся только своей кристаллической структурой, превращение называется бездиффузионным. К бездиффузионным превращениям относятся полиморфные превращения в однокомпонентных системах, а также в некоторых сложных по составу фазах – химических соединения стехиометрического состава и так называемое массивное превращение в твердых растворах. Кинетически при этом различают нормальное полиморфное и мартенситное превращения.
Кинетика некоторых превращений в твердом состоянии названа «нормальной», поскольку как временная, так и температурная зависимости скорости превращения оказались подобными тем, которые ранее были установлены при исследовании процесса кристаллизации. При понижении температуры (для реакций, идущих при охлаждении) скорость превращения сначала увеличивается, а затем уменьшается. Возрастание скорости превращения связано с облегчением образования зародышей и ускорением их роста при увеличении переохлаждения, поскольку при этом возрастает термодинамический стимул превращения; уменьшение скорости превращения при дальнейшем увеличении переохлаждения объясняется уменьшение подвижности атомов при понижении температуры.
Термодинамический стимул превращения определяется полным изменением свободной энергии системы при образовании новой фазы: ∆nФ (n) для области новой фазы, состоящей из n атомов.
Движущей силой процесса роста области новой фазы называют величину d∆Ф(n)/dn; рост области новой фазы происходит, если при увеличении п ∆Ф(п) уменьшается, т. е. d∆Ф(п)/dn<0. Из термодинамики неравновесных процессов получим следующее общее выражение для скорости роста:
dп/dt = – (K /T) п ´d ∆Ф (n)/dn(250)
где n – число атомов, составляющих поверхность раздела области новой фазы и матрицы;
К – кинетический фактор, который определяется механизмом процесса роста.
Рост области новой фазы при бездиффузионном превращении состоит в присоединении к новой фазе атомов, находящихся непосредственно у поверхности раздела фаз. Нормальная кинетика предполагает, что присоединяются (и, наоборот, отрываются) отдельные атомы и эти акты присоединения (или отрыва) никак не связаны.
В процессе перехода атома от одной фазы к другой возникают некоторые промежуточные конфигурации, обладающие повышенной свободной энергией по сравнению с исходным состоянием. Такая конфигурация называется активированным комплексом. На рисунке 106, а состоянию активированного комплекса соответствует максимум, высота которого обозначена [∆Ф(п)+∆Ф(п+1)]/2+q; величина q, характеризующая уровень активированного комплекса, имеет порядок энергии активации процесса самодиффузии. Значения q1 и q2 определяют энергетические барьеры переходов атомов соответственно при увеличении и уменьшении объема частицы новой фазы.
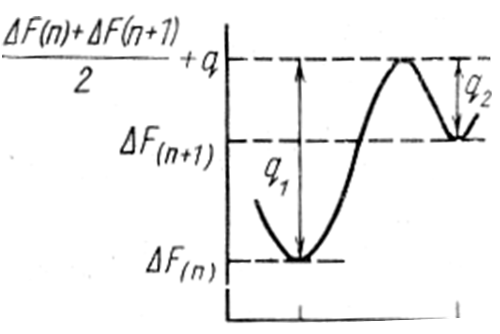
Рисунок 106 – Энергетический барьер у поверхности частицы новой фазы,
характеризующий состояние «активированного комплекса» при присоединении к новой фазе атома
d∆Ф(n)/dn<∆T (251)
для скорости изменения радиуса R сферической частицы было получено (без учета упругой энергии) следующее выражение:
dR/dt=(К/Т)ехр(-q/kT)∆Fo(1-Rкр/R). (252)
где ∆Fo – изменение химической свободной энергии на единицу объема,
К – коэффициент, который включает параметр, характеризующий частоту колебаний атомов (например, температуру Дебая),
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.