Мартенситные превращения. Мартенситное превращение в сплавах на основе железа. Строение мартенсита в сплавах с цветными и благородными металлами, страница 4

R_кр=2α/∆F_o – радиус критического зародыша, зависящий от поверхностного натяжения α.

Как видно из уравнения (252), в соответствии с общей теорией образования фаз рост частицы возможен при R>Rкр.

Температурная зависимость скорости роста, схематически представлена на рисунке 107, в общем, согласуется с экспериментальными данными для разных систем.

Кинетика мартенситного превращения характеризуется обычно очень большой скоростью роста отдельных кристаллов и максимальной объемной скоростью в начальный момент превращения в изотермических условиях. На предварительно полированной поверхности металлографического шлифа, появляется рельеф, связанный с образованием единичных кристаллов. Важнейшая особенность мартенситного механизма превращения – это слабая зависимость подвижности границы фаз от температуры: мартенситное превращение может идти при весьма низких температурах. Во многих случаях развитие превращения в изотермических условиях не наблюдается и превращение идет только по мере охлаждения; такую кинетику иногда называют «атермической» или «взрывной».

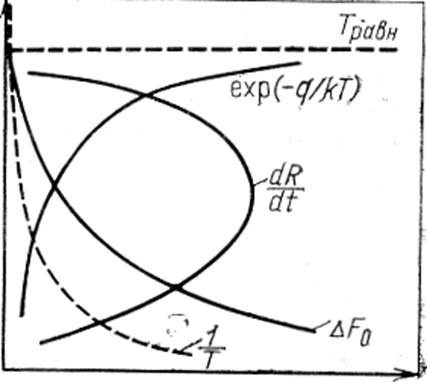
Рисунок 107 – Температурные зависимости кинетических коэффициентов

1/Т и К~-ехр(-q/kT), термодинамического стимула ∆F_o и скорости роста dR/dТ центра новой фазы для «нормального» превращения

Формальное объяснение слабой температурной зависимости скорости мартенситного роста следует из анализа уравнения бездиффузионного превращения (250), если вместо условия (251) принять условие

d∆Ф (п) / dп » kT                                                      (253)

Очень большие значения термодинамической движущей силы характерны для мартенситных превращений, идущих при больших переохлаждениях. Условие (253) дает

dп/dt=-пvexp {-q+1/2[d∆Ф(п)/dп]}/kT.                           (254)

Как видно из уравнения (254), эффективная энергия активации процесса роста меньше величины q на 1/2d∆Ф(п)/dп (d∆Ф(п)/дп<0).

О скорости движения фронта превращения можно судить по времени образования отдельного кристалла. Время роста мартенситного кристалла из аустенита в стали около 10^-7 с при конечном размере кристалла приблизительно 10^-2 см, что соответствует скорости движения межфазовой границы порядка 10⁵ см/с, что близко к скорости звука. Такая большая скорость перестройки решетки обеспечивается согласованным (кооперативным) движением атомов.

Перемещения атомов в кристаллической решетке не могут быть независимыми. Только при достаточно высокой температуре, когда тепловые колебания приводят к значительным нерегулярным смещениям атомов в кристаллической решетке, движение атомов может иметь более или менее автономный характер. С понижением температуры влияние межатомного взаимодействия становится все сильнее и перемещение атомов приобретает все более организованный, кооперативный характер. Обязательным условием кооперативного движения фронта реакции превращения границы раздела новой и исходной фаз – должна быть строгая регулярность расположения атомов на границе. Это достигается при когерентности решеток, когда атомные плоскости в решетке новой и исходной фаз, параллельные границе раздела фаз, имеют одинаковое расположение атомов.

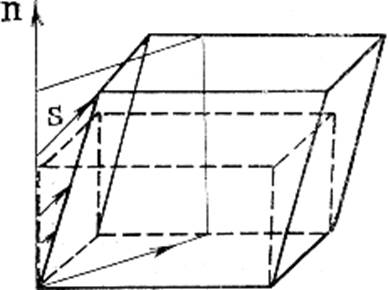
 а                                                                                б                             

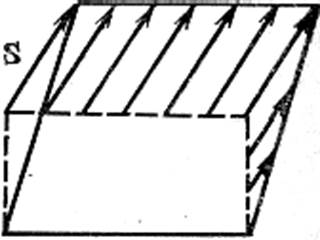
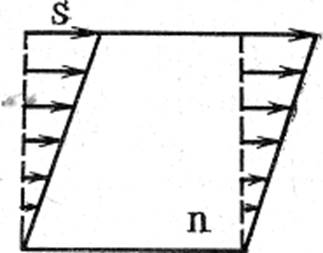
 в                                                                  г

а – сложная однородная деформация объема; б – дилатация (растяжение);

в – сдвиг; г – сдвиг и дилатация

Рисунок 108 – Пример деформации с инвариантной плоскостью. Стрелки показывают направления деформации s и ее величину

Если перестройку решетки при образовании новой фазы представлять как деформацию решетки с инвариантной плоскостью, то инвариантной плоскостью является граница между когерентными областями новой и исходной фаз.

На межфазовой границе имеет место скачок деформации Е, отличающей новую фазу от исходной:

∆ε=1/2(s_on+ns_о).                                                   (255)

где s – вектор направления смещения атомов;

n – нормаль к инвариантной плоскости;