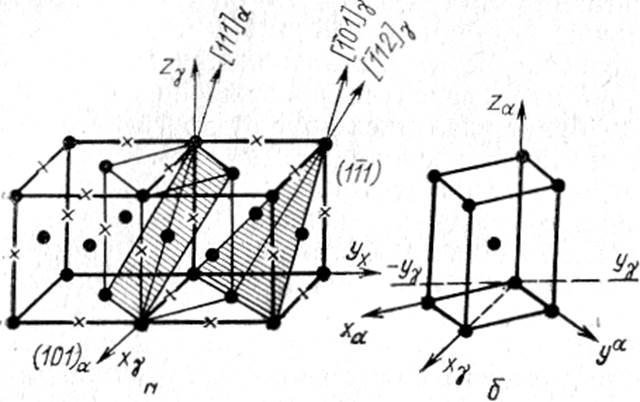
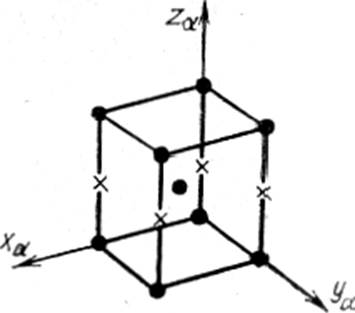
Для записи условия соответствия решеток аустенита мартенсита их следует представить элементарными ячейками, содержащими одинаковое число атомов и требующими минимальной деформации для перехода одной решетки в другую, т. е. ячейка, выделенная в решетке аустенита, должна быть возможно более близкой к конечной ячейке мартенсита. На рисунке 121 приведена сдвоенная г. ц. к. ячейка γ-фазы (аустенита). Такую решетку (оси хγ, уγ, zγ) можно описать как о. ц. т. решетку (оси ха, уа, za)с размерами ячейки: αо.ц.т.=bо.ц.т=αг.ц.к. √2 и со.ц.т.=αг.ц.к; c∕α=1,43. Такое представление целесообразно для анализа, деформации решетки при полиморфном превращении и означает, что именно узлы, выделенные на схеме (рисунок 121б), в результате деформации решетки при превращении примут конфигурацию элементарной ячейки решетки мартенсита (о.ц.к. в безуглеродистых сплавах, например Fe-Ni, тетрагональная – при наличии углерода).
Соответствие решеток аустенита и мартенсита удобно записать в матричной форме. Такая запись позволяет определить кристаллографические индексы направлений при изменении системы координат.
Как известно, кристаллографическое направление определяется как направление вектора из начала координат, координаты конца вектора, упирающегося в узел решетки, являются кристаллографическими индексами данного направления [uυω]α. Можно определить индексы этого же направления в другой координатной системе [uυω]γ, если известна матрица перехода:
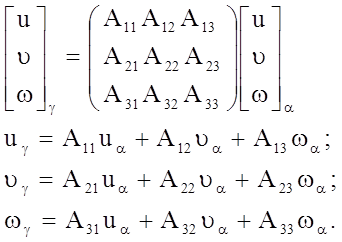 (258)
(258)
Для получения матрицы перехода от системы координат решетки мартенсита к системе координат решетки аустенита запишем координатные направления решетки мартенсита (ха, уа, za) или направления ребер элементарной ячейки - [100]М, [010]M и [001]M – в координатной системе решетки аустенита. Если векторы ребер элементарной ячейки мартенсита 1'1, 1'2 и ľ3, а единичные векторы координатной системы аустенита 11, 12 и 13, то из рисунка 121б следует:
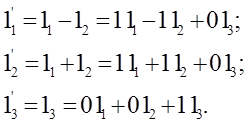 (259)
(259)
Коэффициенты правых частей этих уравнений образуют матрицу перехода от системы координат аустенита к системе координат мартенсита:
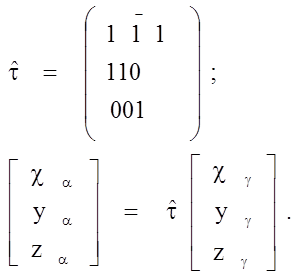 (260)
(260)
Матрица обратного перехода τ получается из матрицы τ заменой столбцов на строки:
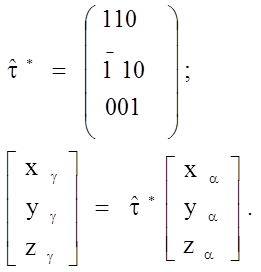 (261)
(261)
Матрицы (260) и (261) позволяют найти соответствующие векторы решеток исходной и новой фаз («соответствующие», т. е. переходящие один в другой при превращении). Чтобы теперь описать изменения длины этих векторов (или координат узлов) решетки при превращении, необходимо найти главные деформации.
Выделенная на рисунке 121б объемноцентрированная тетрагональная (о.ц.т.) ячейка характеризуется степенью тетрагональности c∕a=1,43. В углеродистом α'-мартенсите, как известно, имеется тетрагональность, но гораздо меньшая и зависящая от содержания углерода; безуглеродистый мартенсит (в хромоникелевой или высоконикелевой стали) имеет кубическую ячейку. Поэтому превращение г.ц.к.→о.ц.к. требует деформации, которую в координатной системе исходной фазы можно записать в виде матрицы:
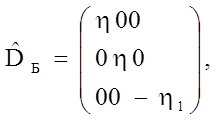 (262)
(262)
где
η = (√2аα - аγ) ∕ аγ; (263)
- η1= (аα - аγ) / аγ. (264)
Эта деформация переводит атомы из узлов г.ц.к. решетки в ближайшие узлы о.ц.к. решетки, объемно-центрированная ячейка, выделенная на рисунке 121б сжимается по оси zα (ось с) и несколько расширяется по осям хα и уα. Для любого вектора rγ решетки γ можно найти соответствующий ему вектор решетки:
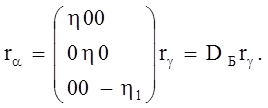 (265)
(265)
С помощью дифракционных методов (рентгенографии и электронографии) всегда удается найти близкие или практически совпадающие (параллельные) кристаллографические направления и плоскости решеток новой и исходной фаз. Из рисунка 121а, видно, что при отсутствии другой деформации (кроме DБ) ориентированную связь γ и α решеток можно записать в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.