1 Структурный анализ механизма комбайна
1.1 Структурная схема механизма (рис.1.1).
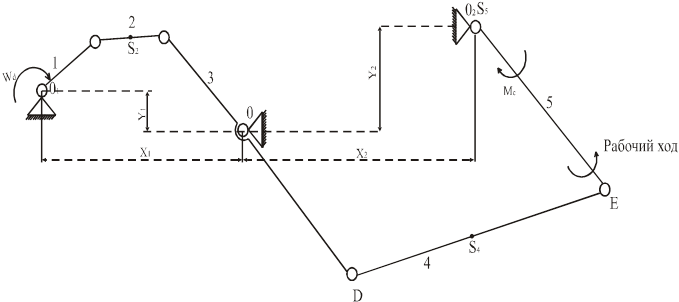 Рис. 1.1
Рис. 1.1
1.2 Классифицируем кинематические пары механизма
Таблица 1.1
|
№ п/п |
Номер звеньев, образую-щих пару |
Условное обозначение |
Название |
Подвиж-ность |
Высшая/ Низшая |
Замыка-ние (Геометрическое/ Силовое) |
Открытая/Закры-тая |
|||
|
|
0 – 1 |
О |
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
1 – 2 |
А |
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
2 – 3 |
B |
Вращательная |
1 |
Н |
Г |
З |
|||
|
4 |
3– 0 |
O
|
Поступательная |
1 |
Н |
Г |
З |
|||
|
|
3 – 4 |
D |
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
4 – 5 |
E |
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
5 – 0 |
О2 |
Вращательная |
1 |
Н |
Г |
З |
Исследуемый механизм состоит только из одноподвижных кинематических пар (р1=р=7), где р1- это число одноподвижных, а р - общее число пар в механизме.
1.3 Классификация звеньев механизма
Таблица 1.2
|
№ п/п |
Номер звена |
Условные обозначения |
Название |
Движение |
Число вершин (t) |
|
1 |
0 |
|
Стойка (0) |
Отсутствует |
- |
|
2 |
1 |
|
Кривошип (1) |
Вращательное |
2 |
|
3 |
2 |
|
Шатун (2) |
Сложное |
2 |
|
4 |
3 |
|
Коромысло (3) |
Вращательное |
3 |
|
5 |
4 |
|
Шатун (4) |
Сложное |
2 |
|
6 |
5 |
|
Кривошип (3) |
Вращательное |
2 |
Механизм имеет 4 (n2=4) двухвершинных (t=2) линейных звена 1,2,3,4,5; одно (n3=1) трехвершинное (t=3) звено 3, которое является базовым. А вообще в механизме имеется пять (n=5) подвижных звеньев.
1.4 Механизм комбайна имеет три (S=3) присоединения к стойке.
1.5 В исследуемом сложном механизме можно выделить один элементарный механизма (рис.1.2).
Рис. 1.2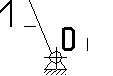
и два простых шарнирных четырехзвенника (рис.1.3)
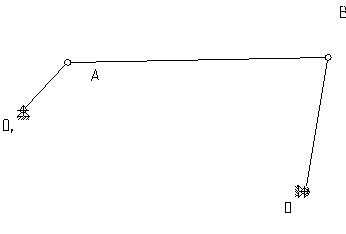
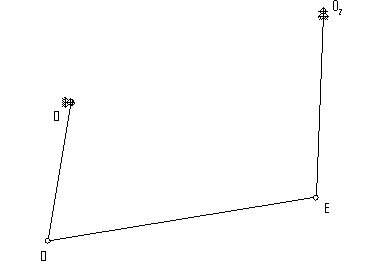
а) б)
Рис. 1.3
Механизмов с разомкнутыми кинематическими цепями в исследуемом механизме комбайна нет.
1.6 При выявлении стационарных и подвижных механизмов обнаружены только простые стационарные механизмы.
1.7 В исследуемом механизме нет звеньев закрепления, а есть только звенья присоединения (коромысло (3)). Звено (3) входит одновременно в два простых механизма – два шарнирных четырехзвенника. Значит для этого звена К3=2.
1.8 Классифицируем механизм комбайна. Механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеет в своем составе только замкнутые кинематические цепи.
1.9 Исследуемый сложный механизм существует в трехподвижном пространстве (П=3).
Определим подвижность шарнирного четырехзвенника. Он имеет три (n=3) подвижных звена, четыре (p=p1=4) одноподвижные кинематические пары. Его подвижность определяется по формулам (1.1):
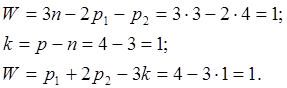 (1.1)
(1.1)
Так как у исследуемого механизма есть два шарнирных четырехзвенника аналогичных по конструкции, то формулы приведенные выше для одного механизма так же верны и для другого.
1.10 Так как в комбайне нет механизмов с незамкнутыми кинематическими цепями, то нет и необходимости определять их подвижность.
1.11 Подвижность сложного механизма комбайна определяется по формулам (1.2):
![]() (1.2)
(1.2)
Так как механизм является однотипным. То его подвижность можно определить по формулам (1.3):
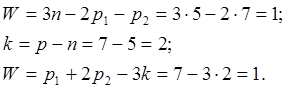 (1.3)
(1.3)
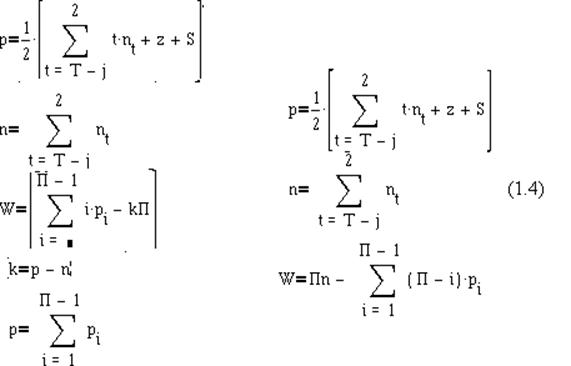 |
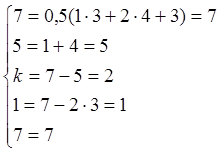
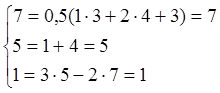
так как уравнения превратились в тождества, то исследуемой устройство имеет правильную структуру и является механизмом.
1.13 Выделяем механизм I класса. В соответствии с классификацией Артоболевского механизм I класса для исследуемого механизма совпадает с элементарным механизмом (рис.1.4).
Рис. 1.4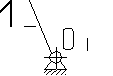
1.14 Выделяем структурные группы Ассура. В механизме их две, но они одинаковы (рис.1.5):
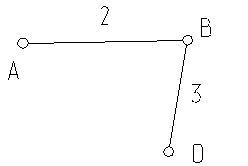
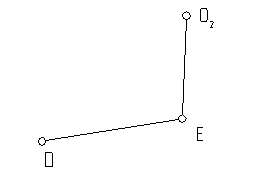
а) б)
Рис.1.5
Они имеют два подвижных звена (n’=2) причем все звенья двухвершинные (t=2) и, значит, базовое звено , так же имеет две вершины (T=2), три (p=3) одноподвижные (p1=3) кинематические пары, из которых две внешние (S’=2).
1.15 Проверяем, соответствуют ли выделенные структурные группы их математическим моделям. Так как группы подобны , то проводим проверку по одной из них , например ABO.
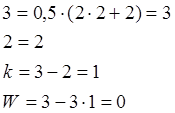
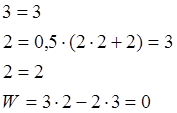
Анализ полученных выражений показывает, что выделенные кинематические цепи являются структурными группами Ассура.
1.16 Проверяем, не распадаются ли выделенные структурные группы на более простые. Видно, что выделенные структурные группы являются самыми простыми для трехподвижного пространства, в котором существует исследуемый механизм, и, значит , они не могут иметь в своем составе другие более простые группы Ассура.
1.17 Проводим классификацию структурных групп по И.И. Артоболевскому.
Таблица 1.3
|
№ п/п |
Структурная схема |
Номер звеньев, образующих группу |
Класс, порядок, вид |
|||||
|
1 |
|
0-1 |
Механизм I класса |
|||||
|
2 |
|
2-3 |
II класс 2 - порядок 1 - вид |
|||||
|
3 |
|
4-5 |
II класс 2 - порядок 1 - вид |
|||||
1.18 Определяем класс сложного механизма станка. Механизм комбайна относится ко II классу.
2 Кинематический анализ механизма комбайна
2.1 Построение планов положений исследуемого механизма
Строим двенадцать планов положений исследуемого механизма комбайна
(Чертёж приложен в конце ПЗ.). Для выбираем масштабный коэффициент длин по
формуле :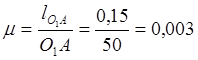 (м/мм),
где
(м/мм),
где ![]() -истинная длина кривошипа,
-истинная длина кривошипа,![]() - чертежный размер кривошипа.
- чертежный размер кривошипа.
Чертежные размеры механизмa
Таблица 2.1
|
O1A, мм |
AB, мм |
BD, мм |
OB, мм |
DE, мм |
O2Е, мм |
X1, мм |
X2, мм |
Y1, мм |
Y2, мм |
|
50 |
333,33 |
250 |
150 |
500 |
150 |
400 |
450 |
50 |
100 |
2.2 Кинематическое исследование машин и механизмов аналитическим способом
Заменим звенья , на вектора произвольного положения и объединим их два замкнутых контура.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.