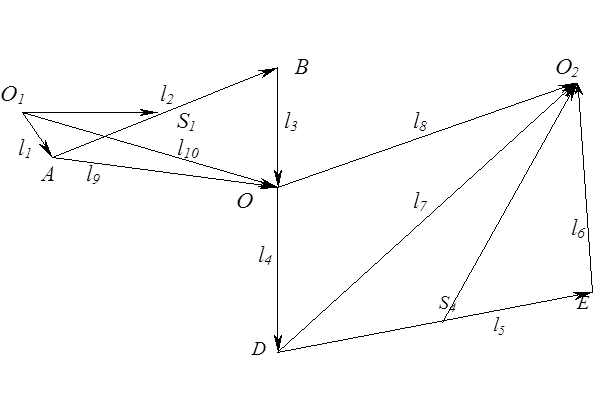
Запишем векторные уравнения.
![]() (2.1)
(2.1) ![]() (2.2)
(2.2)
где значения векторов указаны ниже в таблице:
Таблица 2.2
|
Известная |
l1 , м |
l2 , м |
l3 , м |
l4 , м |
l5 , м |
l6 , м |
l8 , м |
l10 , м |
|
Значение |
0,15 |
0,1 |
0,45 |
0,30 |
1,5 |
0,45 |
1,383 |
1,209 |
Для векторов l8 , l10 значения углов постоянны и равны:
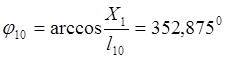
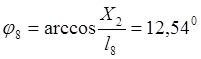
Спроектируем векторные уравнения замкнутости контуров на оси X, Y, получим базовые системы уравнений для определения кинематических характеристик звеньев и их отдельных точек.
|
l1cos(j1)+l2cos(j2)+l3cos(j3)-l10cos(j10)=0 |
(2.3) |
|
l1sin(j1)+l2sin(j2)+l3sin(j3)-l10sin(j10)=0 |
|
l4cos(j4)+l5cos(j5)+l6cos(j6)-l8cos(j8)=0 |
(2.4) |
|
l4sin(j4)+l5sin(j5)+l6sin(j6)-l8sin(j8)=0 |
Среди этих величин j1 является обобщенной координатой механизма, и поэтому должен быть задан.
Решим систему уравнений (2.3) и (2.4) :
1) Найдем углы начала и конца рабочего хода:
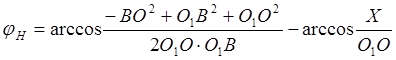 ,
где
,
где ![]() , значит
, значит ![]()
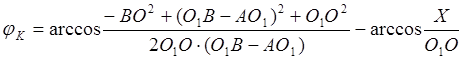 Отсюда
Отсюда
![]()
Для упрощения решения
системы (2.3) введем еще два векторных контура: Первый: ![]() (2.4)
(2.4)
|
l1cos(j1)+l9cos(j9)-l10cos(j10)=0 |
(2.5) |
|
l1sin(j1)+l9sin(j9)-l10sin(j10)=0 |
|
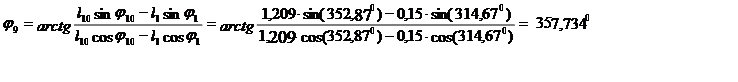
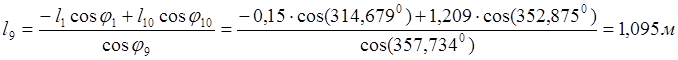
Второй:
![]() (2.6)
(2.6)
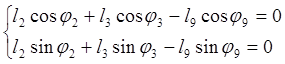 (2.7)
(2.7)
![]()
![]() (2.8) где
(2.8) где
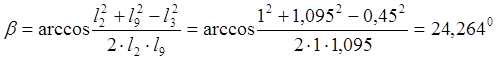
![]()
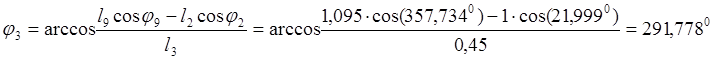
Для решения упрощения системы (2.4) введем еще два векторных контура:
Первый: ![]() (2.9)
(2.9)
|
l4sin(j4)+l7sin(j7)-l8sin(j8)=0 |
(2.10) |
|
l4cos(j4)+l7cos(j7)-l8cos(j8)=0 |
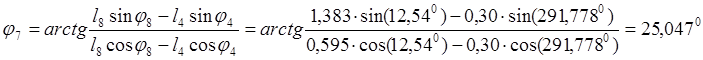
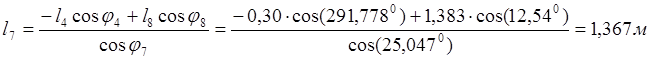
Второй: ![]() (2.11)
(2.11)
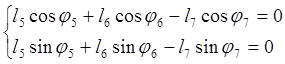 (2.12)
(2.12)
![]()
![]() (2.13)
(2.13)
где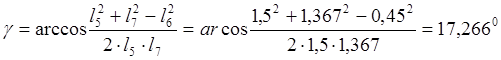 ;
;
![]()
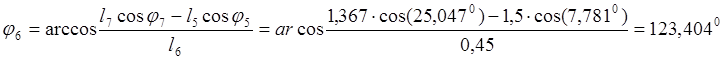
Найдем центры масс звеньев 2, 4. Составляем замкнутые контура:
![]() (2.14)
(2.14)
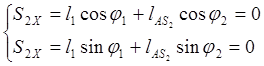 (2.15)
(2.15)
![]() (2.16)
(2.16)
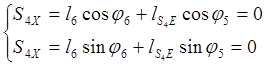 (2.17)
(2.17)
где 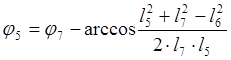 (2.18)
(2.18)
Ниже приведена таблица со значениями неизвестных величин для всех 13 положений механизма.
Таблица 2.3
|
Величина |
j1o |
j9o |
j3o |
j7o |
j6o |
l9 , M |
l7 , M |
|
1 |
14,679 |
349,894 |
281,156 |
24,714 |
115,852 |
1,071 |
1,422 |
|
2 |
344,679 |
354,030 |
284,134 |
24,846 |
117,917 |
1,061 |
1,407 |
|
3 |
314,679 |
357,734 |
291,778 |
25,047 |
123,404 |
1,095 |
1,367 |
|
4 |
284,679 |
359,761 |
301,668 |
24,982 |
130,438 |
1,162 |
1,316 |
|
5 |
254,679 |
359,755 |
311,168 |
24,536 |
137,354 |
1,239 |
1,267 |
|
6 |
224,679 |
358,050 |
318,787 |
23,887 |
142,764 |
1,307 |
1,230 |
|
7 |
194,679 |
355,241 |
322,595 |
23,462 |
145,494 |
1,349 |
1,212 |
|
13 |
188,229 |
354,556 |
322,768 |
23,441 |
145,653 |
1,354 |
1,211 |
|
8 |
164,679 |
351,973 |
320,885 |
23,662 |
144,272 |
1,358 |
1,220 |
|
9 |
134,679 |
348,876 |
313,122 |
24,395 |
138,801 |
1,330 |
1,257 |
|
10 |
104,679 |
346,591 |
302,374 |
24,962 |
130,997 |
1,272 |
1,312 |
|
11 |
74,679 |
345,749 |
291,886 |
25,049 |
123,406 |
1,197 |
1,367 |
|
12 |
44,679 |
346,846 |
284,034 |
24,842 |
117,913 |
1,122 |
1,407 |
Высчитываем погрешность измерений расчетного положения на чертеже от полученных результатов при вычислении
Таблица 2.4
|
Величина |
j1o |
j9o |
j3o |
j7o |
j6o |
l9 , M |
l7 , M |
|
Графически |
314,67 |
357,72 |
291,45 |
25 |
123,1 |
1,07 |
1,35 |
|
Аналитически |
314,679 |
357,734 |
291,778 |
25,047 |
123,404 |
1,095 |
1,367 |
|
D=((A1-A2)/A2)*100% |
0,00286 |
0,00391 |
0,11254 |
0,188 |
0,24695 |
2,33645 |
1,25926 |
Нахождение скоростей аналитическим способом.
Продифференцируем систему уравнений (2.3) для первого векторного контура по обобщенной координате, учитывая что j10=const, l10=const,, получим:
|
-l1j1|sin(j1)-l2j2|sin(j2)-l3j3|sin(j3)=0 |
(2.19) |
|
l1j1|cos(j1)+l2j2|cos(j2)+l3j3|cos(j3)=0 |
Так как звено 1 вращается по часовой стрелки, то j1|=-1
|
l1sin(j1)-l2j2|sin(j2)-l3j3|sin(j3)=0 |
(2.20) |
|
-l1cos(j1)+l2j2|cos(j2)+l3j3|cos(j3)=0 |
Из выше приведенных уравнений получим выражения для нахождения аналогов скоростей звеньев (2) и (3).
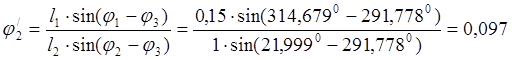
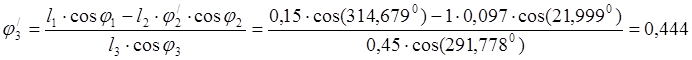
Продифференцируем систему уравнений (2.4) для второго контура по обобщенной координате, учитывая, что j8=const, l8=const, j3=j4 получим:
|
-l4j4|sin(j4)-l5j5|sin(j5)-l6j6|sin(j6)=0 |
(2.21) |
|
l4j4|cos(j4)+l5j5|cos(j5)+l6j6|cos(j6)=0 |
Из выше приведенных уравнений получим выражения для нахождения аналогов скоростей звеньев (5) и (6).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.