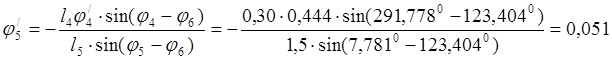
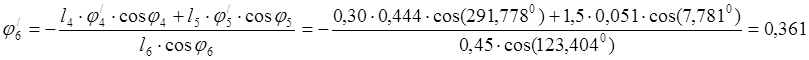
Машиностроение \ Теория машин и механизмов

Структурный анализ механизма комбайна, страница 3

Ниже приведена таблица аналогов скоростей звеньев для 13 положений

Таблица 2.5

Величина	j₂^\|	j₃^\|	j₅^\|	j₆^\|
1	0,250	0,000	0,000	0,000
2	0,218	0,275	0,036	0,220
3	0,097	0,444	0,051	0,361
4	-0,074	0,482	0,045	0,395
5	-0,224	0,423	0,030	0,346
6	-0,301	0,290	0,014	0,234
7	-0,271	0,062	0,002	0,049
13	-0,250	0,000	0,000	0,000
8	-0,144	-0,242	-0,011	-0,194
9	-0,009	-0,469	-0,031	-0,383
10	0,086	-0,534	-0,049	-0,438
11	0,156	-0,457	-0,052	-0,372
12	0,216	-0,274	-0,036	-0,220

Рассчитываем аналоги скорости центров масс. Для этого продифференцируем уравнения координат центров масс:

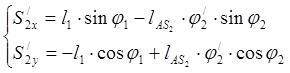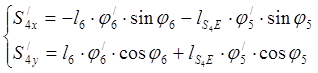(2.22)

Ниже приведена таблица аналогов скоростей центров масс для 13 положений

Таблица 2.6

Величина	S^/_2X	S^/_4X	S^/_2Y	S^/_4y
1	0,015	0,000	-0,058	0,000
2	-0,049	-0,081	-0,066	-0,032
3	-0,094	-0,126	-0,063	-0,066
4	-0,109	-0,125	-0,047	-0,092
5	-0,098	-0,097	-0,019	-0,095
6	-0,066	-0,059	0,015	-0,072
7	-0,020	-0,011	0,052	-0,016
13	-0,009	0,000	0,059	0,000
8	0,035	0,047	0,081	0,061
9	0,085	0,105	0,082	0,109
10	0,114	0,138	0,051	0,103
11	0,111	0,129	0,005	0,069
12	0,075	0,081	-0,034	0,032

Нахождение ускорений аналитическим способом.

Для нахождения аналогов ускорений рассмотрим те же контура, что и при нахождении аналогов скоростей.

Продифференцируем систему уравнений (2.3) для первого контура по обобщенной координате дважды (учитывая что j₁^|,=-1) получим:

-l₁cos(j₁)- l₂j₂^//sin(j₂)- l₂^/(j₂^\|)²cos(j₂)-l₃j₃^//sin(j₃)-l₃(j₃^/)²cos(j₃)=0	(2.23)
-l₁sin(j₁)+ l₂j₂^//cos(j₂)- l₂^/(j₂^/)²sin(j₂)+l₃j₃^//cos(j₃)-l₃(j₃^/)²sin(j₃)=0

вычитаем j₃

Упростим систему уравнений подставив известные значения.

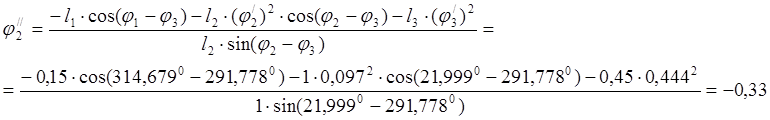
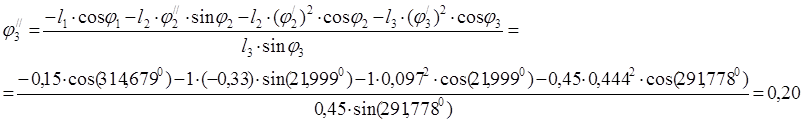
Продифференцируем дважды систему уравнений (2.4) для второго контура учитывая что, j₃=j₄, получим:

-l₄j₄^//sin(j₄)+ l₄(j₄^/)²cos(j₄)- l₅j₅^//sin(j₅)+l₅(j₅^/)²cos(j₅)-l₆j₆^//sin(j₆)-l₆(j₆^/)²cos(j₆)=0	(2.24)
l₄j₄^//cos(j₄)- l₄(j₄^/)²sin(j₄)+ l₅j₅^//cos(j₅)-l₅(j₅^/)²sin(j₅)+l₆j₆^//cos(j₆)-l₆(j₆^/)²sin(j₆)=0	(2.24)

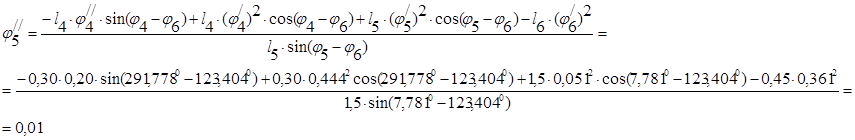
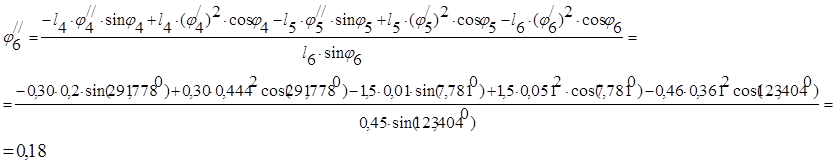
Ниже приведена таблица аналогов ускорений звеньев для 13 положений

Таблица 2.7

Величина	j₂^\|\|	j₃^\|\|	j₅^\|\|	j₆^\|\|
1	0,02	0,60	0,08	0,48
2	-0,16	0,48	0,06	0,39
3	-0,33	0,20	0,01	0,18
4	-0,37	-0,02	-0,02	0,00
5	-0,27	-0,12	-0,02	-0,10
6	-0,09	-0,23	-0,02	-0,19
7	0,14	-0,46	-0,02	-0,37
13	0,18	-0,51	-0,02	-0,41
8	0,26	-0,52	-0,03	-0,42
9	0,17	-0,22	-0,03	-0,18
10	0,10	0,07	-0,01	0,07
11	0,09	0,29	0,02	0,26
12	0,09	0,49	0,06	0,40

Рассчитываем аналоги ускорений центров масс. Для этого продифференцируем уравнения которые мы получили при нахождении аналогов скоростей центров масс.

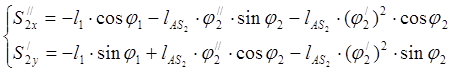(2.25)

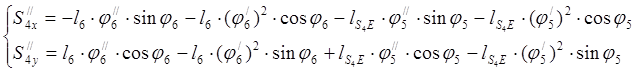(2.26)

Ниже приведена таблица аналогов ускорений центров масс для 13 положений

Таблица 2.8

Величина	S^//_2X	S^//_2Y	S^//_4X	S^//_4Y
1	-0,13	-0,03	-0,18	-0,06
2	-0,11	-0,01	-0,13	-0,07
3	-0,06	0,01	-0,03	-0,08
4	0,00	0,03	0,04	-0,05
5	0,04	0,05	0,06	-0,01
6	0,07	0,06	0,07	0,04
7	0,09	0,06	0,09	0,12
13	0,10	0,06	0,10	0,13
8	0,10	0,03	0,11	0,12
9	0,08	-0,04	0,09	0,01
10	0,03	-0,09	0,03	-0,08
11	-0,04	-0,10	-0,06	-0,10
12	-0,10	-0,07	-0,14	-0,08

1 2 3 4 5

Скачать файл