Структурный анализ механизма комбайна, страница 5

При движении звена различные его точки в общем случае имеют различные ускорения. По принципу Даламбера к каждой точке звена, обладающей элементарной массой dm, следует приложить элементарную силу инерции , где а – ускорение массы dm. Так как звено имеет множество точек, то и сил инерции, действующих на звено, – множество. На практике при расчете самого звена на прочность ограничиваются конечным числом сил инерции, которые сосредотачивают в центрах тяжести. В дальнейшем обычно эти силы приводят к центру масс S звена. В результате на центр масс звена действует результирующая сила инерции (главный вектор инерции), называемая силой инерции F_И, и главный момент сил инерции звена (момент пары сил инерции) М_И. Сила инерции F_И и момент пары сил инерции М_И определяются по формулам соответственно:

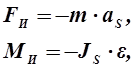
где m – масса звена; а_S – вектор ускорения центра масс; J_S – момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения; e – угловое ускорение звена. Знак минус показывает, что сила и момент инерции направлены противоположно ускорению.

Находим для исследуемого станка угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.

Для начального звена в первом положении  соответственно будем иметь

Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающими их с аналогами скоростей и ускорений, которые имеют следующий вид:

;   ;       .         (3.1)

Ускорение центра масс и угловое ускорение, например, второго звена, в соответствии с последними формулами (4.1) определится:

;.    

Результаты расчета ускорений других звеньев механизма по формулам (3.1) приведены в табл. 3.1.

Таблица 3.1.

Ускорения центров масс и угловые ускорения звеньев.

Определив ускорения звеньев, находим главный вектор и главный момент сил инерции звеньев механизма. Тогда соответственно главный вектор сил инерции и главный инерционный момент звеньев механизма определится:

Для звена 1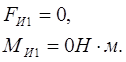               

Для звена 2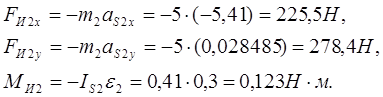               

Для звена 4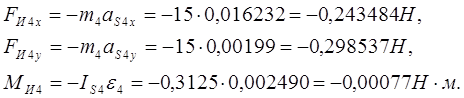               

Для звена 5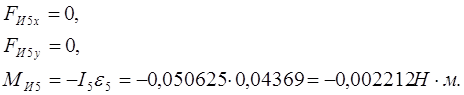           

3.1.2. Силы, действующие на механизм.

Для удобства дальнейшей работы в табл. 3.2 сведены все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.

Силы и моменты, действующие на механизм.

Таблица 3.2

	Сила веса, Н				Силы инерции, Н					Моменты сил инерции, Н×м
Мc,	F2y	F3y	F4y	F5y	FИ2x	FИ2y	FИ4x	FИ4y	FИ3x	МИ1	МИ2	МИ4	МИ5
30	-29,43	0	-147,15	-29,43	0,060738	-0,0854	-0,2434	-0,0298	0	0	-0,0017	-0,000778	-0,0022

Так как направления сил и моментов учтены их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а моменты – против хода часовой стрелки.

3.2. Определение уравновешивающего момента  и реакции в кинетических парах аналитическим методом

3.2.1.Силовой анализ структурной группы 4-5.

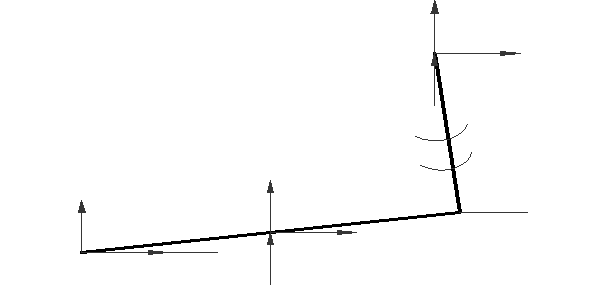Рисуем структурную группу 4-5 (рис. 3.1). прикладываем к ней с целью упрощения вычислений в проекциях на оси действующие на нее силы. Действие на звено 5 со стороны стойкой 0 заменяем реакциями R_50x и R_50y, а на звено 4 со стороны звена 3 – реакциями R_43x и R_43y. Записываем в проекциях на оси координат условия равновесия всех сил, действующих на звенья 4 и 5:

Рис. 3.1. Силовой анализ структурной группы 4-5  аналитическим методом.

1.  , 

, 

2.   Находим сумму моментов относительно точки Е для звена 4

,

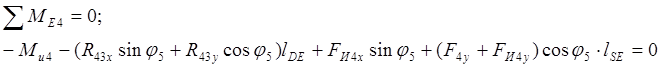3.   Находим сумму моментов относительно точки D для звена 5

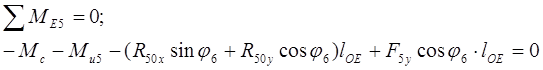
Переносим все известные величины вправо и подставим численные значения и получим:

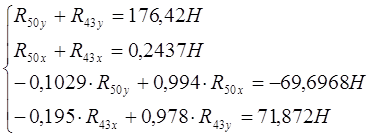
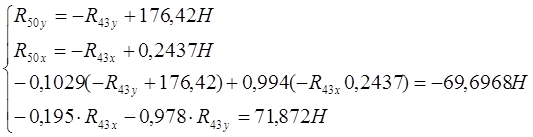
Решая систему уравнений, находим:

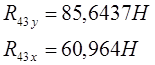
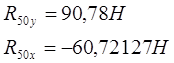
4.   Записываем в проекциях на оси координат условия равновесия всех сил, действующих в шарнире Е:

, откуда

.

, откуда

.

3.2.2. Силовой анализ структурной группы 2–3.

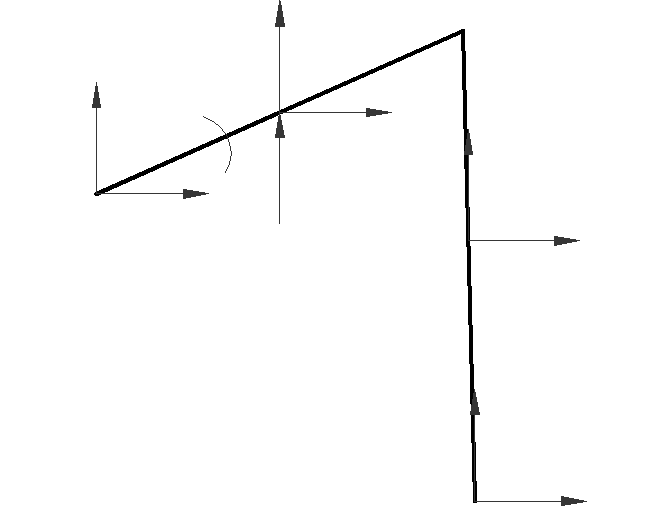
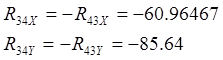
1.  , 

, 

2.   Находим сумму моментов относительно точки В для звена 3

,

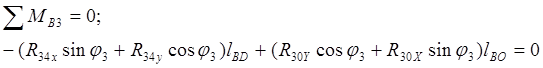3.   Находим сумму моментов относительно точки В для звена 2

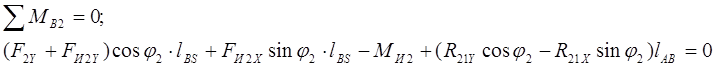
Переносим все известные величины вправо и подставим численные значения и получим:

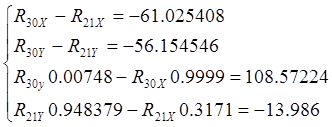
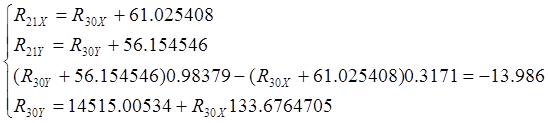
      Решая систему находим:

               

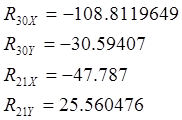
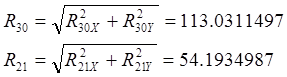
Записываем в проекциях на оси координат условия равновесия всех сил, действующих в шарнире В:

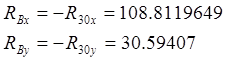
3.2.4. Определение уравновешивающего момента M_y и реакции R₁₀ в кинематической паре 0 - 1.

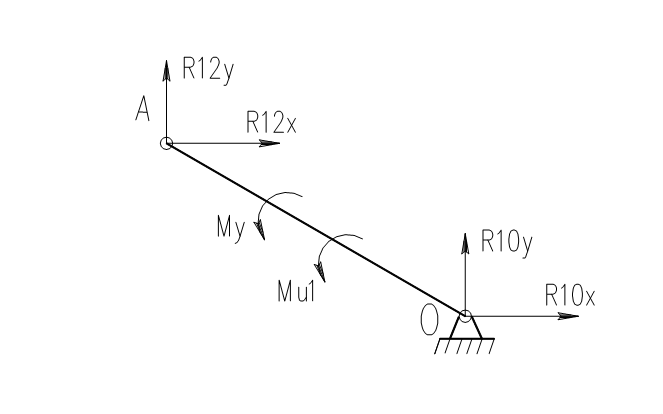Рис.3.3

Для этого составляем уравнения равновесия начального звена механизма. (рис. 3.3). Эти уравнения имеют следующий вид:

                  

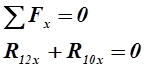
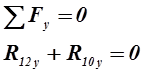
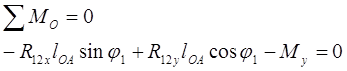
где , ; ,  – проекции на оси координат реакции на звено 1 стойки 0;  – длина первого звена;  – уравновешивающий момент.

Решая записанные выше уравнения, найдем

 

Полная реакция в опоре О₁ будет определяться следующим образом:

.