2.7. Функции от многомерных случайных величин
Рассмотрим двумерную случайную величину ![]() и однозначную числовую функцию
и однозначную числовую функцию ![]() . Определим новую случайную величину
. Определим новую случайную величину ![]() по следующему правилу:
по следующему правилу:
![]() , которую
естественно назвать функцией от случайных величин
, которую
естественно назвать функцией от случайных величин ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
2.7.1. Функции от дискретных случайных величин
Если случайная величина ![]() -
дискретная, то случайная величина
-
дискретная, то случайная величина ![]() тоже будет дискретной,
так как множество её значений не "больше", чем множество возможных
значений случайной величины
тоже будет дискретной,
так как множество её значений не "больше", чем множество возможных
значений случайной величины ![]() . Причём закон
распределения случайной величины будет иметь вид:
. Причём закон
распределения случайной величины будет иметь вид:
|
|
|
|
… |
|
|
|
|
|
… |
|
![]() .
.
Если появляются одинаковые значения в первой строке,
то соответствующие столбцы таблицы заменяются одним и возможному значению
приписывается суммарная вероятность. Так как, если ![]() , то
, то
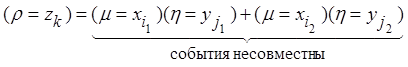
![]()
![]() .
.
2.7.2. Функции от непрерывных случайных величин
Для
непрерывной двумерной случайной величины ![]() с
плотностью распределения вероятностей
с
плотностью распределения вероятностей ![]() функция
распределения, как и ранее, определяется равенством
функция
распределения, как и ранее, определяется равенством
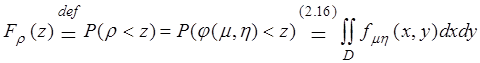 , (2.18)
, (2.18)
где
![]() область, определяемая неравенством
область, определяемая неравенством ![]() .
.
Композицией случайных величин называется случайная величина, равная сумме этих величин.
Если композиция случайных величин, распределённых по одному и тому же закону распределения, является случайной величиной, распределённой по тому же закону, то закон распределения называется композиционно устойчивым.
Пусть ![]() – независимые случайные
величины, рассмотрим случайную величину
– независимые случайные
величины, рассмотрим случайную величину ![]() (используем
функцию
(используем
функцию ![]() ).
).
Найдём функцию распределения ![]() случайной
величины
случайной
величины ![]() .
.
По формуле (2.18) (рис. 2.5):
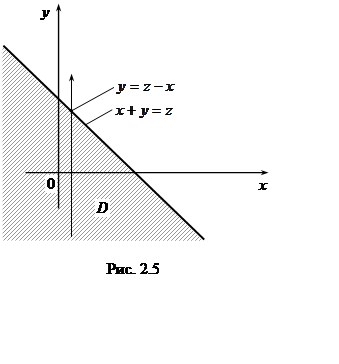
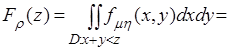
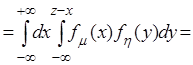
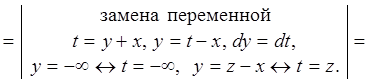
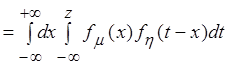 .
.
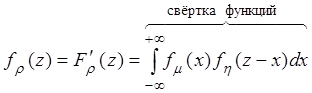 (2.19)
(2.19)–
выражение плотности распределения вероятностей случайной величины ![]() . Интеграл, стоящий в правой части
равенства (2.19), называется сверткой функций и обозначается
. Интеграл, стоящий в правой части
равенства (2.19), называется сверткой функций и обозначается ![]() .
.
2.8. Числовые характеристики дискретных случайных величин
Пусть ![]() – дискретная случайная
величина, заданная законом распределения.
– дискретная случайная
величина, заданная законом распределения.
Математическим ожиданием случайной величины ![]() называется
число, равное сумме попарных произведений возможных значений случайной величины
на вероятности, с которыми эти значения принимаются. Обозначается:
называется
число, равное сумме попарных произведений возможных значений случайной величины
на вероятности, с которыми эти значения принимаются. Обозначается: ![]() .
.
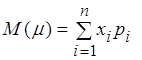 . (2.20)
. (2.20)
Выясним смысл этой характеристики. Пусть в N
испытаниях случайная величина ![]() принимает значение
принимает значение ![]() раз,
раз, ![]() раз, …,
раз, …,
![]() раз. Найдём сумму всех значений, принимаемых
случайной величиной в этих испытаниях
раз. Найдём сумму всех значений, принимаемых
случайной величиной в этих испытаниях 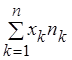 , а
затем найдём среднее арифметическое
, а
затем найдём среднее арифметическое
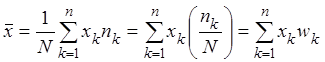 .
.
При ![]() :
: ![]() (см. статистическое определение
вероятности), следовательно при
(см. статистическое определение
вероятности), следовательно при  .
.
Таким образом, математическое ожидание ![]() приближенно равно (и тем точнее, чем
больше число испытаний) среднему значению, принимаемому случайной величиной.
приближенно равно (и тем точнее, чем
больше число испытаний) среднему значению, принимаемому случайной величиной.
Свойства ![]() :
:
![]() .
. ![]() , с– const.
, с– const.
Доказательство. Постоянную с можно рассматривать как дискретную случайную
величину с единственным возможным значением, которое принимается с вероятностью
равной 1. Поэтому по формуле (2.20) ![]() .
.
![]() .
. ![]() (используемая функция
(используемая функция ![]() ).
).
Доказательство. По формуле (2.20): 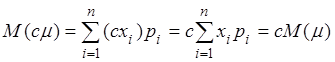 .
.
![]() .
. ![]() (используемая функция
(используемая функция ![]()
![]() ).
).
Доказательство. По формуле (2.20):
![]()
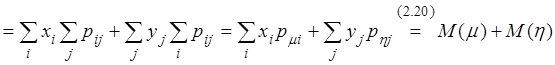 .
.
![]() . Если
. Если ![]() – независимые случайные величины, то
– независимые случайные величины, то
![]() .
.
Доказательство. Так как ![]() – независимые случайные
величины, то
– независимые случайные
величины, то
![]()
Величина, характеризующая разброс возможных значений случайной величины относительно среднего значения, называется дисперсией.
Обозначается: ![]() .
.
По определению дисперсия равна математическому
ожиданию квадрата отклонения случайной величины от её математического ожидания ![]() :
:
![]() ,
,
(используемая
функция ![]() .
.
Используя свойства математического ожидания, получаем формулу
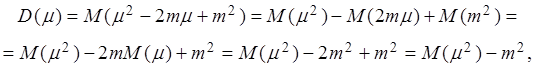
![]() (2.21)
(2.21)
Свойства дисперсии:
![]() .
. ![]() .
.
Доказательство. Используя формулу (2.21), получаем:
![]() .
.
![]() .
. ![]() .
.
Доказательство. Используя формулу (2.21), можем записать:
![]() .
.
![]() . Если
. Если ![]() – независимые случайные величины, то
– независимые случайные величины, то
![]() .
.
Доказательство. Используем формулу (2.21):
![]()
=![]()
![]()
![]()
40 ![]() .
.
Доказательство. Используем формулу (2.21):
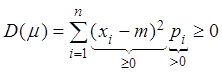 .
.
Нетрудно видеть, что дисперсия имеет размерность квадрата случайной величины. Для практических расчетов удобно иметь меру разброса, размерность которой совпадает с размерностью случайной величины. В качестве такой меры используется среднее квадратическое отклонение.
Средним квадратическим отклонением ![]() случайной величины
случайной величины ![]() называется корень квадратный из дисперсии,
т.е. по определению
называется корень квадратный из дисперсии,
т.е. по определению ![]() .
.
2.8.1. Числовые характеристики основных законов распределения
Равномерное распределение
|
|
1 |
2 |
3 |
… |
n |
|
P |
|
|
|
… |
|
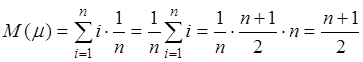
(использована формула суммы n членов арифметической прогрессии).
![]()
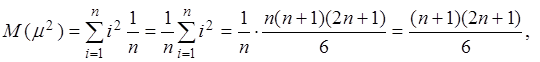
 ,
, 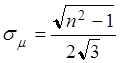 .
.
(использована формула суммы квадратов первых nнатуральных чисел).
Биноминальное распределение
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.