Условное математическое ожидание ![]() зависит от того, какое из возможных
значений принимает случайная величина
зависит от того, какое из возможных
значений принимает случайная величина ![]() , т. е.
от
, т. е.
от ![]() , следовательно
, следовательно ![]() –
случайная величина непрерывного типа.
–
случайная величина непрерывного типа.
Функция ![]() называется регрессией
случайной величины
называется регрессией
случайной величины ![]() на случайную величину
на случайную величину ![]() .
.
Свойства условного математического ожидания:
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]() Если
Если ![]() – условно независимые величины,
относительно случайной величины
– условно независимые величины,
относительно случайной величины ![]() (это означает, что
(это означает, что ![]() и
и ![]() независимы
при каждом значении случайной величины
независимы
при каждом значении случайной величины ![]() ), тогда
), тогда
![]() .
.
![]()
![]() .
.
Доказательство. Рассмотрим, например, дискретный случай.По определению ![]()
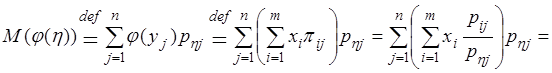
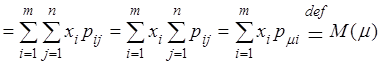 .
.
![]()
![]() .
.
Доказательство. Для любого фиксированного номера возможного значения j можем записать
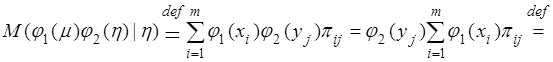
![]() .
.
Так
как ![]() – произвольно, то получаем доказываемое
свойство.
– произвольно, то получаем доказываемое
свойство.
![]() Если
Если ![]() , тогда
, тогда
![]() .
.
Доказательство. Рассмотрим опять дискретный случай.Пусть ![]() – возможные значения случайной величины
– возможные значения случайной величины ![]() , тогда
, тогда
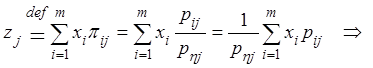
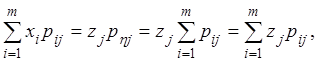
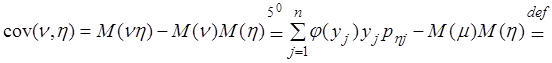
=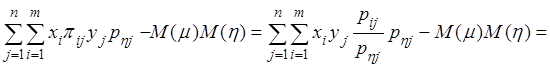
![]() .
.
2.11.4. Линейная регрессия
Во многих случаях регрессия случайной величины ![]() на случайную величину
на случайную величину ![]() , т.е. функция
, т.е. функция ![]() близка
к линейной, поэтому зависимость
близка
к линейной, поэтому зависимость ![]() можно заменить линейной
зависимостью
можно заменить линейной
зависимостью ![]() .
.
Возникает вопрос: как выразить параметры этой
зависимостиa и ![]() ?
?
Для получения параметров используется принцип метода
наименьших квадратов, т. е. a и ![]() выбираются из условия
выбираются из условия
![]()
Откуда, записывая необходимое условие существования экстремума, получаем систему уравнений относительно параметров
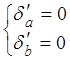 ,
,
![]()
![]()
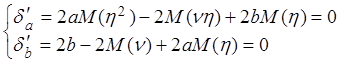 , или
, или 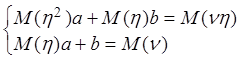 .
.
Решая эту систему, например по формулам Крамера, находим:
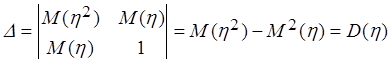 ,
,
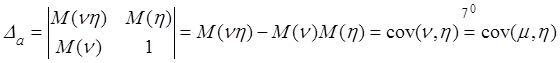 ,
,
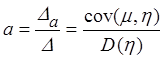 .
.
Из второго уравнения системы
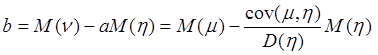 .
.
Таким образом, уравнение линейной регрессии случайной
величины ![]() на случайную величину
на случайную величину ![]() будет иметь вид:
будет иметь вид:
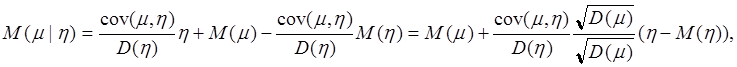
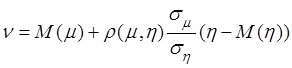 . (2.25)
. (2.25)
Величина 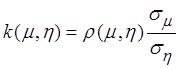 называется коэффициентом
линейной регрессии.
называется коэффициентом
линейной регрессии.
Аналогично
можно получить уравнение линейной регрессии случайной величины ![]() на случайную величину
на случайную величину ![]() , оно имеет вид:
, оно имеет вид:
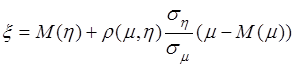 , где
, где
![]() .
.
2.12. Закон больших чисел
Ранее было отмечено, что нельзя предвидеть, какое из возможных значений примет случайная величина, так как мы не можем учесть все обстоятельства, от которых зависит это событие. Однако в некоторых случаях можно указать вероятность такого события. События, вероятность которых мала, редко происходят, а события, вероятность которых близка к единице, происходят почти обязательно.
Принцип, заключающийся в том, что маловероятные события на практике рассматриваются как невозможные, носит название "принципа практической невозможности маловероятных событий". События, вероятности которых близки к единице, считаются практически достоверными (принцип практической достоверности).
Следовательно, одной из задач теории вероятностей является установление закономерностей, происходящими с вероятностями, близкими к единице или к нулю. Всякое утверждение, устанавливающее отмеченные закономерности, называется законом больших чисел.
Лемма
Маркова. Пусть ![]() – случайная величина,
принимающая лишь неотрицательные значения, тогда справедливо неравенство:
– случайная величина,
принимающая лишь неотрицательные значения, тогда справедливо неравенство:
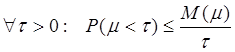 .
(2.26)
.
(2.26)
Доказательство. Это неравенство справедливо как для непрерывных, так и для дискретных случайных величин. Рассмотрим, для определенности, случай непрерывной случайной величины.
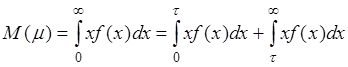 .
.
Оба слагаемых в правой части неотрицательны, поэтому
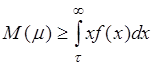 , но
теперь
, но
теперь ![]() , следовательно
, следовательно
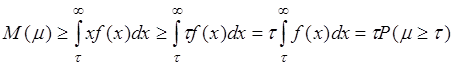 , отсюда,
так как
, отсюда,
так как ![]() , получаем неравенство (2.26).
, получаем неравенство (2.26).
Неравенство Чебышева. ![]() справедливо неравенство:
справедливо неравенство:
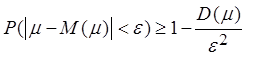 .
(2.27)
.
(2.27)
Это неравенство справедливо как для непрерывных, так и для дискретных случайных величин.
Так как события ![]() и
и ![]() несовместны и противоположны, то
несовместны и противоположны, то ![]() .
.
Подставляя вероятность ![]() ,
выраженную через вероятность противоположного события, в левую часть
неравенства (2.27), получаем эквивалентную запись неравенства Чебышева
,
выраженную через вероятность противоположного события, в левую часть
неравенства (2.27), получаем эквивалентную запись неравенства Чебышева
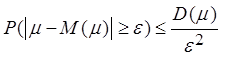 . (2.28)
. (2.28)
Доказательство. Для определенности пусть ![]() - дискретная случайная
величина. Рассмотрим и оценим дисперсию этой случайной величины.
- дискретная случайная
величина. Рассмотрим и оценим дисперсию этой случайной величины.
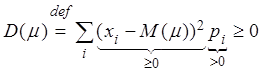 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.