Функции от многомерных случайных величин. Дополнительные числовые характеристики случайных величин. Распределения, связанные с нормальным распределением, страница 2

Здесь случайную величину можно рассматривать как сумму независимых случайных величин ,  где  – число появлений события А в i–м испытании. Закон распределения каждой из них имеет вид

Отсюда получаем:

 .

Так как  – независимые случайные величины, то

,

,    .

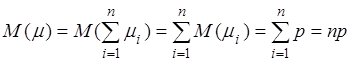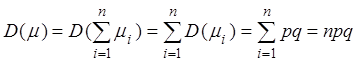Распределение Пуассона

   ,

 

,  .

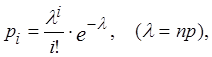
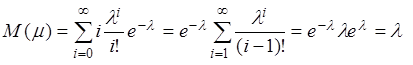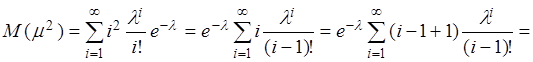
Геометрическое распределение

, ,

.

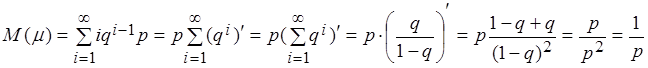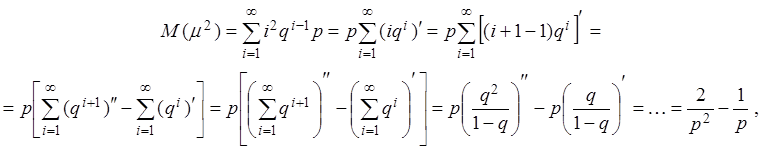
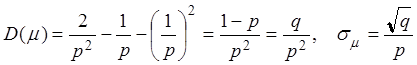2.9. Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины  с плотностью распределения вероятностей  называется число , равное

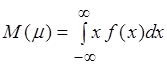
Как и в дискретном случае, здесь  – среднее значение случайной величины

Свойства :

. , с – const.

.  (используемая функция )

.  (используемая функция  ).

. Если  – независимые случайные величины, то

.

Доказательство.

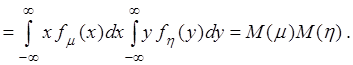
По определению дисперсия равна математическому ожиданию квадрата отклонения случайной величины от её математического ожидания

,

,

.

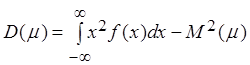Числовые характеристики основных законов распределения

Равномерное распределение

 .

.

,  .

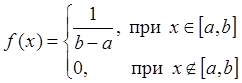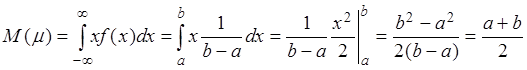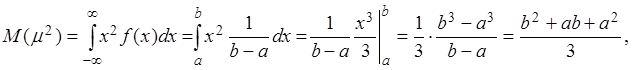
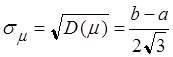Показательное (экспоненциальное) распределение

.

,

,      .

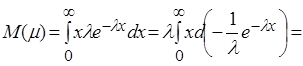
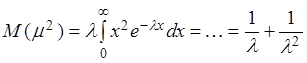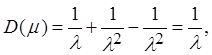
При вычислении  дважды используется формула интегрирования по частям.

Нормальное распределение

.

   .

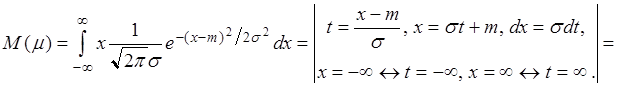
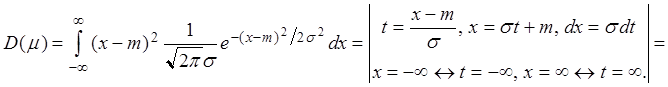
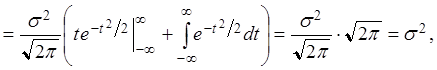
2.10. Дополнительные числовые характеристики

случайных величин

Начальным моментом -го порядка  называется математическое ожидание -й степени случайной величины , т. е.

.

Центральным моментом -го порядка  называется математическое  ожидание -й степени отклонения случайной величины  от её математического ожидания:

Например,

.

Коэффициентом асимметрии –  называется величина, равная отношению центрального момента третьего порядка к кубу среднего квадратичного отклонения

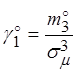
Коэффициент асимметрии характеризует несимметричность распределения относительно математического ожидания. Для симметричного распределения

.

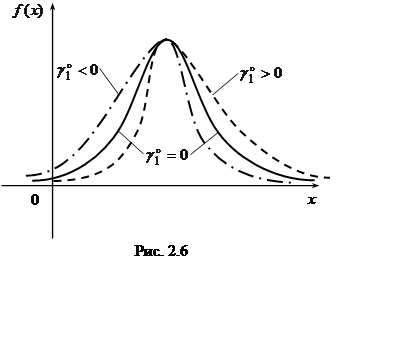Если для некоторого распределения , то это распределение не симметрично относительно среднего значения. Геометрическая интерпретация приведена на рис. 2.6.

Коэффициентом эксцесса –  называется величина, равная отношению центрального момента четвертого порядка к четвертой степени среднего квадратичного отклонения за вычетом числа 3

.

Для нормального распределения 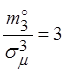, то есть .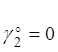

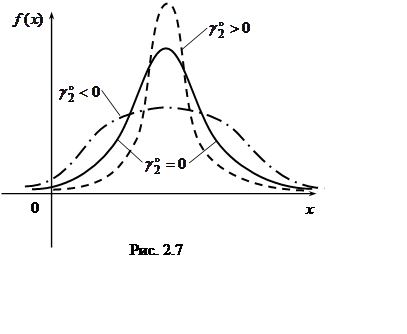
Коэффициент эксцесса характеризует скорость изменения плотности вероятности случайной величины (рис. 2.7). ,  – безразмерные величины.

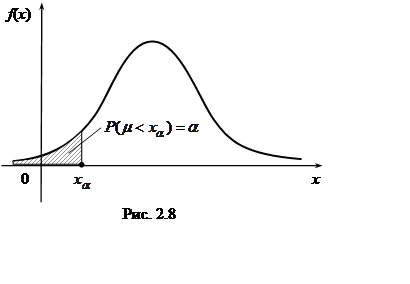
Квантилью уровня  или -квантилью –  называется наибольшая величина, которая удовлетворяет неравенству (рис. 2.8):

       Для непрерывного распределения неравенство заменяется равенством.

            Для дискретной случайной величины  – максимальное значение, при котором выполняется неравенство (*).

Если 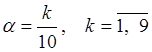, то  называются децилями. Квантиль  называется медианой.

Для симметричного распределения медиана совпадает с математическим ожиданием.

Абсцисса точки локального максимума плотности распределения вероятностей случайной величины называется модой .

Рассмотрим двумерную случайную величину  и определим характеристику связи между  и , которая называется ковариацией.

Ковариацией называется математическое ожидание произведения центрированных случайных величин  и . Для них

.

Обозначается: .

Таким образом, по определению

или

.

                              (2.22)

Свойства ковариации:

 .

 Если  – независимые случайные величины, то

.

Доказательство.

Обратное утверждение, вообще говоря, неверно, т.е. существуют случайные величины, для которых , но эти случайные величины являются зависимыми.

Пример 2.10. Подбрасываются две игральные кости. Случайные величины  – числа очков, выпавших соответственно на первой и второй игральных костях.

Пусть  – сумма и разность выпавших очков. Найти .

Решение. По формуле (2.22) находим (случайные величины , очевидно, распределены одинаково)

.