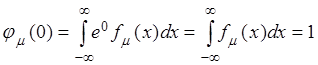 , последнее
равенство есть условие нормировки плотности распределения вероятностей.
, последнее
равенство есть условие нормировки плотности распределения вероятностей.
20. Если ![]() , то
, то ![]() .
.
Доказательство. Действительно
![]()
![]() .
.
30. Если случайные величины ![]() и
и ![]() –
независимы, то
–
независимы, то
![]() .
.
Доказательство. Так как ![]() – независимые случайные
величины, то и функции
– независимые случайные
величины, то и функции ![]() тоже будут независимыми
случайными величинами, следовательно, по свойствам математического ожидания:
тоже будут независимыми
случайными величинами, следовательно, по свойствам математического ожидания:
![]()
![]() .
.
40. Если существует начальный момент
порядка n для случайной величины ![]() , то
, то
![]() :
: ![]()
Доказательство. Пусть ![]() – непрерывная случайная
величина, тогда по условию существует начальный момент порядка n
– непрерывная случайная
величина, тогда по условию существует начальный момент порядка n
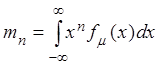 ,
, 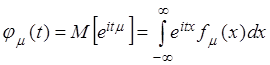 .
.
Существование ![]() позволяет
позволяет
![]() дифференцировать правую часть равенства по
дифференцировать правую часть равенства по
![]() как по параметру:
как по параметру:
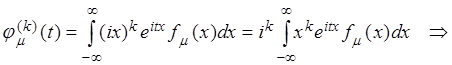
Þ 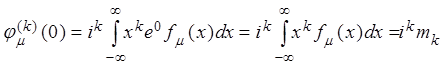 .
.
При изучении закона больших чисел было показано, что
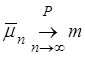 .
.
Требуется определить закон распределения ![]() . Если
. Если ![]() одинаково
распределены, то
одинаково
распределены, то
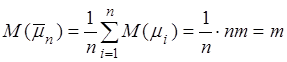 .
.
Пусть ![]() – последовательность
независимых одинаково распределённых случайных величин.
– последовательность
независимых одинаково распределённых случайных величин.
Рассмотрим нормированную и центрированную случайную величину
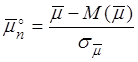 , здесь
, здесь ![]() ,
, ![]() .
.
Центральная предельная теорема. При ![]() справедливо
соотношение:
справедливо
соотношение:
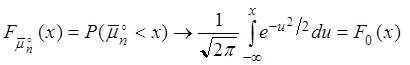 , где
, где
![]() – функция распределения стандартного
нормального закона.
– функция распределения стандартного
нормального закона.
Доказательство.
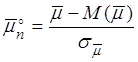 .
. ![]() ,
, 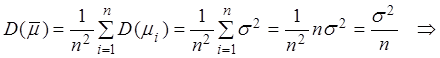
Þ 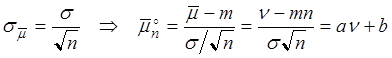 , где
, где
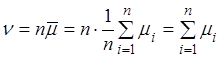 ,
, 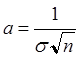 ,
, 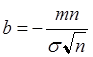 .
.
Обозначим характеристическую функцию случайной
величины ![]() через
через ![]() , а
случайной величины
, а
случайной величины ![]() через
через ![]() ,
тогда
,
тогда
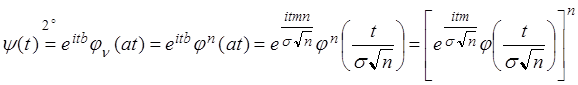 .
.
Найдём ![]() :
:
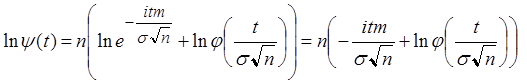 .
.
Запишем формулу Маклорена второго порядка для функции ![]() ,
, 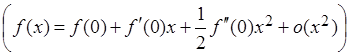 , где
, где 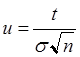 .
.
![]() ;
; 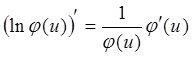 ,
, 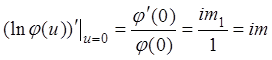 ,
,
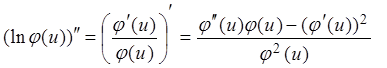 ,
,
 .
.
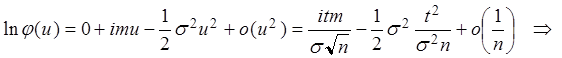
Þ 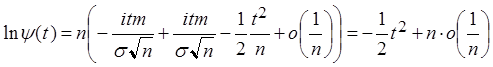 , по
определению
, по
определению ![]() :
: 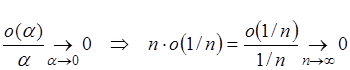 ,
тогда из последнего соотношения
получаем
,
тогда из последнего соотношения
получаем
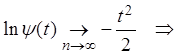
![]()
–
характеристическая функция стандартного нормального закона распределения,
значит ![]() – распределена по стандартному нормальному
закону.
– распределена по стандартному нормальному
закону.
2.14*. Распределения, связанные с нормальным распределением
Рассмотрим несколько распределений, которые широко используются в математической статистике (в следующей главе курса).
2.14.1. Распределение ![]() (хи-квадрат)
(хи-квадрат)
Рассмотрим n независимых случайных величин,
распределённых по стандартному нормальному закону, т.е. с параметрами ![]() . Построим новую случайную величину
. Построим новую случайную величину ![]() , определив ее с помощью равенства
, определив ее с помощью равенства
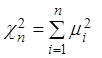 .
.
Распределение этой случайной величины носит название ![]() -распределения (хи-квадрат) с n
степенями свободы. Получим закон распределения этой случайной величины. При n
= 1, получаем
-распределения (хи-квадрат) с n
степенями свободы. Получим закон распределения этой случайной величины. При n
= 1, получаем ![]() ,
,
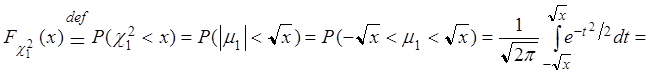
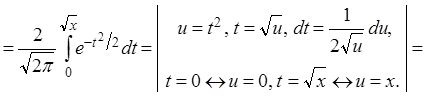
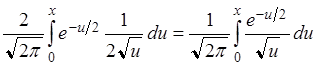 ,
,
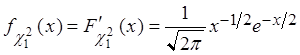 .
.
Методом математической индукции покажем, что
![]() .
.
При ![]() равенство получено.
равенство получено.
Предполагаем, что при произвольном n эта
формула справедлива, покажем, что она справедлива и при ![]()
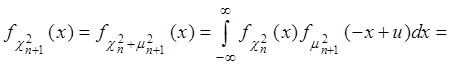
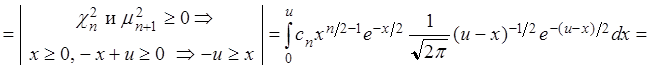
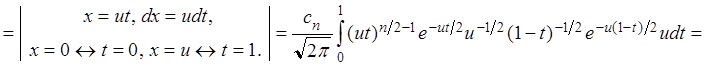
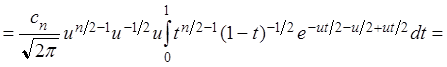
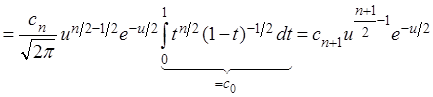 .
.
Постоянную ![]() найдём из условия
нормировки
найдём из условия
нормировки
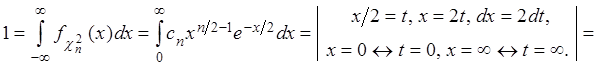
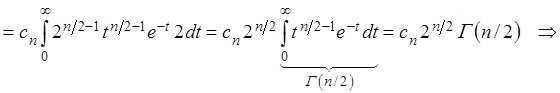
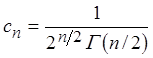 .
.
Таким образом, плотность распределения вероятностей случайной величины хи-квадрат с n степенями свободы имеет вид
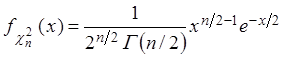 .
.
В математической статистике используется следующий факт.
Если ![]() – независимые
одинаково распределенные случайные величины, подчиненные нормальному закону с
одинаковыми параметрами: математическим ожиданием m, дисперсией
– независимые
одинаково распределенные случайные величины, подчиненные нормальному закону с
одинаковыми параметрами: математическим ожиданием m, дисперсией ![]() , тогда случайная величина
, тогда случайная величина
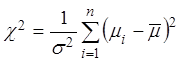 , где
, где
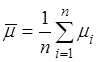 , имеет
, имеет ![]() -распределение,
но с n – 1 степенями свободы.
-распределение,
но с n – 1 степенями свободы.
2.14.2. Распределение Стьюдента (t-распределение)
Пусть ![]() и
и ![]() – независимые случайные величины, причем
– независимые случайные величины, причем ![]() – случайная величина, распределённая по
стандартному нормальному закону,
– случайная величина, распределённая по
стандартному нормальному закону, ![]() – случайная величина с
законом распределения хи-квадрат с n степенями свободы. Распределение случайной
величины
– случайная величина с
законом распределения хи-квадрат с n степенями свободы. Распределение случайной
величины
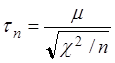
называется распределением Стьюдента (t-распределением) с n степенями свободы.
Плотность распределения Стьюдента имеет вид
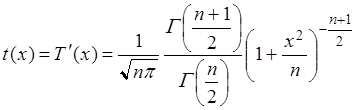 .
.
В математической статистике используется следующий факт.
Если ![]() – независимые
одинаково распределенные случайные величины, подчиненные нормальному закону с
математическим ожиданием m, то случайные величины
– независимые
одинаково распределенные случайные величины, подчиненные нормальному закону с
математическим ожиданием m, то случайные величины 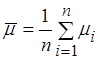 и
и 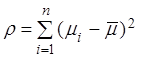 также
независимы, а случайная величина
также
независимы, а случайная величина
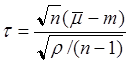
имеет распределение Стьюдента с n – 1 степенями свободы.
2.14.3. Распределение Фишера (F-распределение)
Пусть
![]() и
и ![]() – две
независимые случайные величины, имеющие
– две
независимые случайные величины, имеющие ![]() -распределение
с m и n степенями свободы соответственно. Распределение случайной
величины
-распределение
с m и n степенями свободы соответственно. Распределение случайной
величины
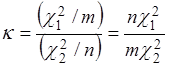
носит название распределения Фишера (F-распределение) с параметрами m и n.
Распределение Фишера имеет плотность
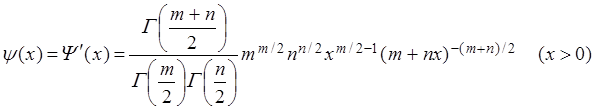 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.