Функции от многомерных случайных величин. Дополнительные числовые характеристики случайных величин. Распределения, связанные с нормальным распределением, страница 3

При этом сумма очков, очевидно, зависит от того, чему равна разность выпавших очков, т.е. случайные величины  являются зависимыми. Так, например,

.

 Если , то .

Доказательство.

 .

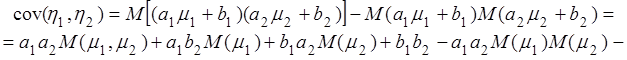
Доказательство.

.

При анализе связей между случайными величинами использование ковариации несколько неудобно, так как размерность этой характеристики равна произведению размерностей случайных величин  и . Поэтому определяется безразмерная характеристика, которая называется коэффициентом корреляции – .

По определению:

.

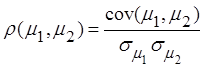Свойства :

 .

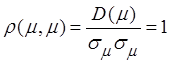 Если случайные величины  – независимы, то .

 Если , то .

 .

Доказательство. Рассмотрим случайную величину  и найдем ее дисперсию.

=  

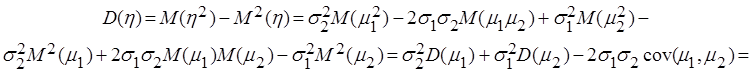
            Аналогично, рассматривая случайную величину , получаем .

 , причём:

если , то ; если , то .

Доказательство. Из доказательства свойства  следует, что если рассмотреть случайную величину , то

.

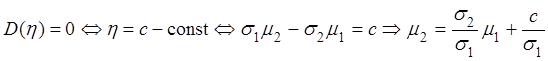  причем  .

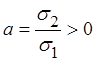Если , то .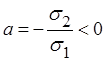

Таким образом, коэффициент корреляции является показателем линейной корреляционной связи случайных величин. Считается, что если:

а)  – слабая связь;

б)  – тесная связь;

в)  – сильная связь.

2.11. Условное распределение и условное математическое ожидание

Рассмотрим двумерную случайную величину .

Если  принимает какое-либо одно из своих возможных значений, то как охарактеризовать распределение случайной величины ?

Используя понятие условной вероятности случайного события, приходим к понятию условного распределения.

2.11.1. Условный закон распределения дискретной случайной величины

Пусть , тогда условной функцией распределения случайной величины  при условии  называется функция

Þ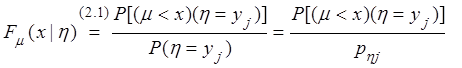                       

Если случайная величина задана законом распределения можно определить условные вероятности

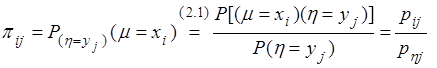,                    (2.23)

и составить условный закон распределения в виде следующей таблицы:

Первый столбец и j-й столбец этой таблицы представляют собой условный закон распределения случайной величины  при , где

.

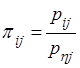Заметим, что    .

2.11.2. Условный закон распределения непрерывной случайной величины

В этом случае формулой (2.23) воспользоваться нельзя, так как ранее было доказано, что .

Найдём вероятность того, что  при условии  и затем перейдем к пределу при :

.

Аналогично:

.

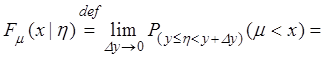
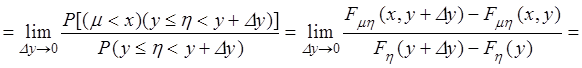
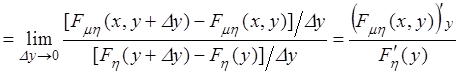Таким образом, приходим к определению условной функции распределения

.

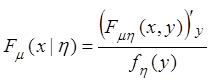Так как  и производная от интеграла с переменным верхним пределом равна подынтегральной функции, то

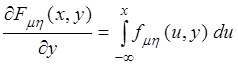
и                                                     .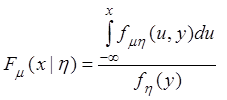                                                    

Очевидно, что у этой функции существует производная по .

Эта производная называется условной плотностью распределения вероятностей случайной величины  при условии ( = y)

.                                                     (2.24)

2.11.3. Условное математическое ожидание случайной величины

Пусть  – дискретная случайная величина.

Условным математическим ожиданием случайной величины  при условии  называется число, определяемое по формуле

.

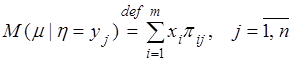Условное математическое ожидание зависит от того, какое из возможных значений принимает случайная величина , т. е. как функция от случайной величины само является случайной величиной. Область определения этой функции совпадает с множеством возможных значений случайной величины : , т.е. это тоже дискретная случайная величина.

Условное математическое ожидание непрерывной случайной величины определяется аналогично дискретному случаю

.

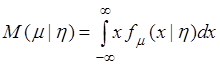Здесь условная плотность распределения вероятностей   вычисляется по формуле (2.24).