Отбросим в сумме часть слагаемых, для которых ![]() . В результате получим:
. В результате получим:

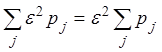 , (2.29)
, (2.29)
где
![]() . В правой части неравенства (2.29)
. В правой части неравенства (2.29)
 .
.
Таким образом, ![]() .
.
Разделив обе части этого неравенства на ![]() , получим неравенство (2.28).
, получим неравенство (2.28).
С помощью аналогичных рассуждений неравенство Чебышева доказывается и для непрерывных случайных величин.
Теорема Чебышева. Пусть ![]() - последовательность независимых
случайных величин с равномерно ограниченной дисперсией, т.е.
- последовательность независимых
случайных величин с равномерно ограниченной дисперсией, т.е.
![]() , тогда
, тогда
![]() , при
, при ![]() выполняется
равенство:
выполняется
равенство:
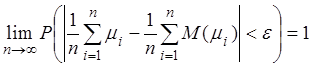 . (2.30)
. (2.30)
Доказательство.
Рассмотрим случайную величину 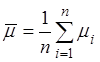 – среднее арифметическое
случайных величин
– среднее арифметическое
случайных величин ![]() , тогда
, тогда 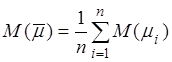 –
среднее арифметическое математических ожиданий. Запишем для этой случайной
величины неравенство Чебышева. Так как
–
среднее арифметическое математических ожиданий. Запишем для этой случайной
величины неравенство Чебышева. Так как ![]() независимые
случайные величины, то
независимые
случайные величины, то
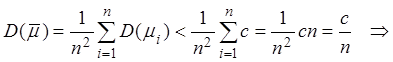
 .
.
Переходя к пределу при ![]() (второе
слагаемое при этом стремится к нулю), получаем
(второе
слагаемое при этом стремится к нулю), получаем
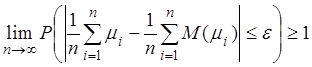 , но
вероятность любого случайного события не может быть больше единицы, следовательно,
справедливо равенство (2.30).
, но
вероятность любого случайного события не может быть больше единицы, следовательно,
справедливо равенство (2.30).
Смысл теоремы заключается в том, что среднее арифметическое большого числа случайных величин утрачивает случайный характер и стремится к числу, равному среднему арифметическому математических ожиданий этих случайных величин.
Частный случай теоремы Чебышева – теорема Бернулли.
Теорема Бернулли. В последовательности из n независимых испытаний
![]() :
: 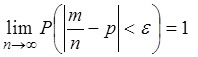 , где
, где
![]() , m – число
появлений события
, m – число
появлений события ![]() в n
испытаниях, т. е.
в n
испытаниях, т. е. 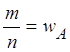 – относительная частота
появления события
– относительная частота
появления события ![]() .
.
Доказательство. Рассмотрим случайную величину
![]() , где
, где
![]() – число появлений события
– число появлений события ![]() в
в ![]() -м
испытании. Законы распределения случайных величин
-м
испытании. Законы распределения случайных величин ![]() одинаковы
и имеют вид:
одинаковы
и имеют вид:
|
|
|
|
|
|
|
|
следовательно:
![]() .
.
В этом случае 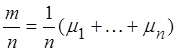 ;
; 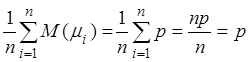 , и
записывая теорему Чебышева, получаем требуемый результат.
, и
записывая теорему Чебышева, получаем требуемый результат.
Пусть имеется последовательность случайных величин ![]() и некоторое неслучайное число
и некоторое неслучайное число ![]() .
.
Если ![]() :
: ![]() , то говорят, что последовательность
, то говорят, что последовательность ![]() по вероятности сходится к
по вероятности сходится к ![]() . При этом используются обозначения:
. При этом используются обозначения:
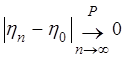 или
или 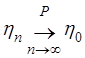 .
.
2.13*. Характеристическая функция и её свойства
Рассмотрим произвольную случайную величину ![]() .
.
Характеристической функцией этой случайной величины называется математическое
ожидание функции ![]() (где
(где ![]() –
мнимая единица,
–
мнимая единица, ![]() ).
).
Обозначается: ![]() .
.
Таким образом,
![]() .
.
Для дискретной случайной величины
 (2.31)
(2.31)
или
![]() , здесь использована формула
Эйлера
, здесь использована формула
Эйлера ![]() .
.
Для непрерывной случайной величины
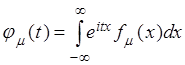 (2.32)
(2.32)
или
 .
.
Формула (2.32) представляет собой с точностью до
постоянного множителя ![]() преобразование Фурье функции
преобразование Фурье функции ![]() . Если записать обратное преобразование
Фурье, то получим, что
. Если записать обратное преобразование
Фурье, то получим, что
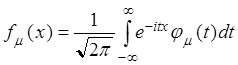
или
для любых точек ![]() и
и ![]() непрерывности
плотности распределения:
непрерывности
плотности распределения:
 .
.
Таким образом, можно установить взаимно однозначное соответствие между характеристическими функциями случайных величин и их плотностями распределения вероятностей (функциями распределений для дискретных случайных величин) или, что то же самое, характеристическая функция однозначно определяет случайную величину.
Простейшие свойства характеристической функции
10. ![]() –
непрерывная функция,
–
непрерывная функция, ![]() .
.
Доказательство. Непрерывность ![]() следует для дискретной случайной
величины с бесконечным множеством значений из равномерной сходимости ряда
следует для дискретной случайной
величины с бесконечным множеством значений из равномерной сходимости ряда
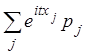 .
.
Этот
ряд сходится равномерно, так как 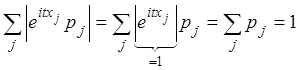 , а, как известно,
равномерно сходящийся ряд из непрерывных функций является непрерывной функцией.
, а, как известно,
равномерно сходящийся ряд из непрерывных функций является непрерывной функцией.
Если дискретная случайная величина имеет конечное
множество значений, то непрерывность функции ![]() очевидна.
Она непрерывна как сумма конечного числа непрерывных функций.
очевидна.
Она непрерывна как сумма конечного числа непрерывных функций.
Непрерывность функции ![]() для
непрерывной случайной величины следует из равномерной сходимости интеграла,
стоящего в правой части равенства (2.31).
для
непрерывной случайной величины следует из равномерной сходимости интеграла,
стоящего в правой части равенства (2.31).
Для дискретной случайной величины:
 .
.
Для непрерывной случайной величины:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.