Глава 3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
3.1. Основные задачи и понятия математической статистики
Установление закономерностей, которым подчиняются случайные массовые явления методами теории вероятности на основе эмпирических (статистических) данных, составляет предмет математической статистики.
Математическая статистика решает две основные задачи:
1) разработку методов сбора, группировки и хранения статистических данных (общая статистика);
2) разработку методов анализа полученных статистических данных:
а) оценку неизвестной вероятности случайного события;
б) оценку неизвестной функции распределения случайной величины;
в) оценку неизвестных параметров распределения при известной функции распределения;
г) оценку зависимости случайных величин от одной или нескольких других случайных величин;
д) проверку статистических гипотез:
– о законе распределения случайной величины;
– о величине параметров распределения случайной величины (при известной функции распределения);
– о совпадении двух распределений;
– о равенстве параметров двух распределений и т.д.
Пусть имеется N объектов произвольной природы, объединённых по некоторому качественному или количественному признаку. Требуется на основе статистических данных установить распределение этого признака.
Наиболее надёжный способ – это полное обследование.
Изучаемая совокупность из N объектов называется генеральной совокупностью.
Выборочной совокупностью или просто выборкой называется nслучайно отобранных объектов.
При таком определении выборки, количественный признак, по которому сформирована генеральная совокупность, является некоторой случайной величиной. Каждому объекту в выборке соответствуют некоторые значения этой случайной величины, которые называются вариантами. Таким образом, выборку можно рассматривать как набор вариант.
С другой стороны, значения вариант от выборки к выборке меняются, т.е. они сами являются случайными величинами. Причём эти случайные величины независимы, одинаково распределены и распределены точно так же, как случайная величина m– количественный признак генеральной совокупности.
Варианты, расположенные в неубывающем порядке, называются вариационным рядом.
Пусть в результате формирования выборки
значение признака, равного х1,наблюдалось n1
раз, значение признака, равного х2,наблюдалось n2 раз, …, значение признака,
равного хm, – nm раз. Числа ni называются
частотами вариант, а 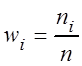 – относительными
частотами
– относительными
частотами ![]() , здесь
, здесь ![]() –
число различных вариант в выборке.
–
число различных вариант в выборке.
Совокупность пар чисел (xi, ni) или (xi, wi) называется статистическим распределением и обычно представляется в виде таблиц:
|
Варианты |
x1 |
x2 |
… |
x m |
или |
Варианты |
x1 |
x2 |
… |
x m |
|
Частоты |
n1 |
n2 |
… |
nm |
Относительные частоты |
w1 |
w2 |
… |
wm |
Статистическое распределение является аналогом закона распределения дискретной случайной величины.
Если количественный признак генеральной совокупности
является непрерывной случайной величиной, трудно ожидать, что в выборке будут
появляться одинаковые варианты (в теории вероятностей было получено, что для
непрерывной случайной величины ![]() – фиксированного
возможного значения), т.е. наиболее вероятно, что все ni = 1. В этом случае строится интервальное статистическое
распределение. Пусть
– фиксированного
возможного значения), т.е. наиболее вероятно, что все ni = 1. В этом случае строится интервальное статистическое
распределение. Пусть ![]() – вариационный ряд, т.е.
– вариационный ряд, т.е.
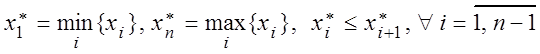 .
.
Этот вариационный ряд разбивается на l промежутков, обычно
равной длины ![]() . При этом
. При этом 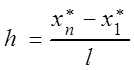 –
шаг разбиения,
–
шаг разбиения, ![]() – граничные точки
промежутков. В качестве частоты
– граничные точки
промежутков. В качестве частоты ![]() принимается число
вариант, попавших в
принимается число
вариант, попавших в ![]() -й промежуток.
-й промежуток.
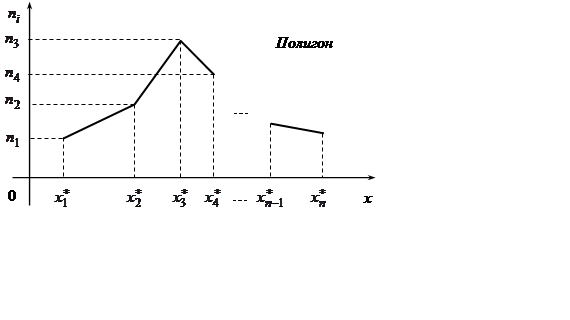 Для графического представления
статистического распределения используется полигон и гистограмма.
Для графического представления
статистического распределения используется полигон и гистограмма.
Полигон – это ломаная, соединяющая точки ![]() или
или
![]() ,
, ![]() .
.
 Для интервального статистического
распределения вместо
Для интервального статистического
распределения вместо ![]() берутся середины
интервалов. Полигон является аналогом плотности распределения случайной
величины, если она непрерывна.
берутся середины
интервалов. Полигон является аналогом плотности распределения случайной
величины, если она непрерывна.
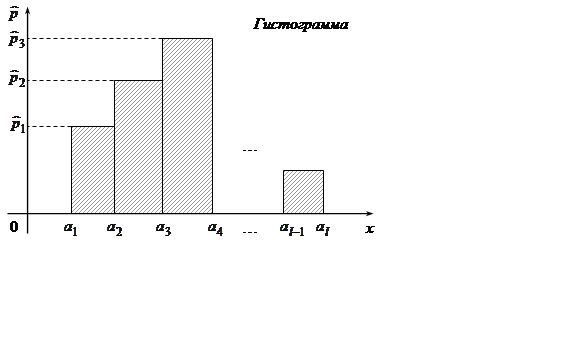
Гистограмма– это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых являются промежутки разбиения, а высотами частоты ![]() или относительные частоты wi или
эмпирические вероятности
или относительные частоты wi или
эмпирические вероятности
 .
.
В последнем случае площадь ступенчатой фигуры равна единице, действительно
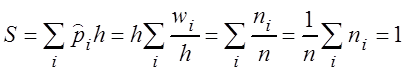 .
.
Пусть nх – число вариант в выборке, которые меньше, чем х.
Функция вида 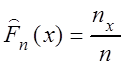 называется
эмпирической функцией распределения.
называется
эмпирической функцией распределения.
Эта функция обладает всеми свойствами функции распределения случайной величины, а именно:
![]() .
. ![]() ;
;
![]() – неубывающая
функция;
– неубывающая
функция;
![]() .
. ![]() .
.
Все свойства легко выводятся непосредственно из определения.
Как функция многомерной случайной величины
эмпирическая функция распределения ![]() , в свою очередь,
тоже является случайной величиной.
, в свою очередь,
тоже является случайной величиной.
"e > 0, "xÎR: 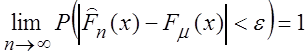 , или
, или 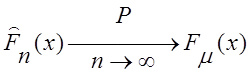 ,
,
где
![]() – теоретическая функция
распределения количественного признака генеральной совокупности.
– теоретическая функция
распределения количественного признака генеральной совокупности.
Доказательство. Для любого фиксированного х с
каждой вариантой выборки хk
можно связать случайное событие Аk = (xk < x). Если появление события ![]() назвать
успехом, то
назвать
успехом, то ![]() – число успехов в
– число успехов в ![]() независимых испытаниях схемы
Бернулли, тогда
независимых испытаниях схемы
Бернулли, тогда
pk = Р(Аk) = Р(хk < x) = Р(m < x) = Fm(x)
– вероятность успеха,
![]() =
= 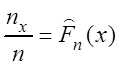
– относительная частота успеха.
Следовательно, по теореме Бернулли:
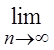 Р(|
Р(|![]() | < e) = 1,
| < e) = 1, ![]()
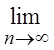 P(|
P(|![]() | < e) = 1.
| < e) = 1.
Вывод:при ![]() эмпирическая функция
распределения утрачивает случайный характер и сколь угодно близко приближается
к теоретической функции распределения.
эмпирическая функция
распределения утрачивает случайный характер и сколь угодно близко приближается
к теоретической функции распределения.
График эмпирической функции распределения выглядит как график функции распределения дискретной случайной величины.
Таким образом, эмпирическая функция распределения – это аналог функции распределения случайной величины.
3.2. Точечные оценки параметров распределения
Предположим,
что в результате наблюдений получена случайная выборка ![]() из
генеральной совокупности с известной функцией распределения.
из
генеральной совокупности с известной функцией распределения. ![]() . Относительно этой функции известно,
что она принадлежит некоторому параметрическому семейству функций распределения,
т.е.
. Относительно этой функции известно,
что она принадлежит некоторому параметрическому семейству функций распределения,
т.е.
![]() ,
,
где q – параметр, который может быть как числовым, так и векторным.
Как правило, если не оговорено противное, будем считать, что ![]() - числовой параметр.
- числовой параметр.
Требуется только по данным случайной выборки найти значение параметра q.
Произвольная функция ![]() =
=![]() (х1,
…, хn), зависящая только от вариант выборки,
значение которой приближенно равно параметру q, называется точечной оценкой этого параметра.
(х1,
…, хn), зависящая только от вариант выборки,
значение которой приближенно равно параметру q, называется точечной оценкой этого параметра.
Оценка ![]() ,
как функция многомерной случайной величины, также является случайной величиной,
функцию распределения которой можно найти, и эта функция распределения будет
также зависеть от параметра q.
,
как функция многомерной случайной величины, также является случайной величиной,
функцию распределения которой можно найти, и эта функция распределения будет
также зависеть от параметра q.
Для непрерывной случайной величины m:
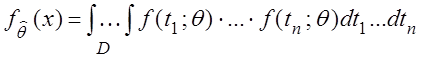 ,
,
где D:![]() , f(x; q) – плотность
распределения случайной величины m.
, f(x; q) – плотность
распределения случайной величины m.
Для дискретной случайной величины строится закон распределения:
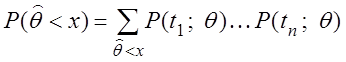 ,
,
где ![]() ,
, ![]() ,
, ![]() –
возможные значения случайной величины m, L – число различных возможных значений.
–
возможные значения случайной величины m, L – число различных возможных значений.
Пример 3.1. В последовательности n испытаний
Бернулли P(A) = p = q. Построить закон распределения оценки параметра ![]() .
.
Решение. Пусть mi – число появлений события А в i–м испытании. Множество возможных значений mi: {0, 1}. Закон распределения mi:
|
mi |
0 |
1 |
|
P |
1–q |
q |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.