![]()
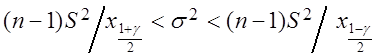 ,
,
где ![]() ,
, ![]() – квантили
– квантили ![]() -распределения с
-распределения с ![]() степенями свободы.
степенями свободы.
3.6. Линейная регрессия
Пусть теперь количественный признак
генеральной совокупности – двумерная случайная величина (m, h). Таким образом, результаты наблюдений (выборка) представляется в
виде n пар чисел (xi,
yi), i = ![]() ,
i – номер наблюдения.
,
i – номер наблюдения.
Предположим, что между компонентами ![]() существует линейная зависимость,
т.е.
существует линейная зависимость,
т.е. ![]() (имеется в виду связь
между всеми возможными значениями величин
(имеется в виду связь
между всеми возможными значениями величин ![]() ,
т.е. для генеральной совокупности).
,
т.е. для генеральной совокупности).
Наличие случайных отклонений, вызванных
воздействием на случайную величину ![]() множества
неучтенных факторов и ошибок измерения, приводит к тому, что связь наблюдаемых
значений
множества
неучтенных факторов и ошибок измерения, приводит к тому, что связь наблюдаемых
значений ![]() случайных величин
случайных величин ![]() приобретает вид
приобретает вид
![]() ,
,
где ![]() – случайные
ошибки (отклонения, возмущения).
– случайные
ошибки (отклонения, возмущения).
Задача состоит в следующем: по имеющимся
данным наблюдений ![]() (двумерной
выборке) оценить значения параметров
(двумерной
выборке) оценить значения параметров ![]() и
и ![]() , обеспечивающих минимум отклонений
наблюдаемых значений от точек прямой
, обеспечивающих минимум отклонений
наблюдаемых значений от точек прямой ![]() .
.
Если бы были известны точные значения ![]() , то параметры
, то параметры ![]() и
и ![]() можно
было рассчитать. Однако значения
можно
было рассчитать. Однако значения ![]() в выборке неизвестны и по наблюдениям
в выборке неизвестны и по наблюдениям ![]() можно
получить лишь точечные оценки
можно
получить лишь точечные оценки ![]() этих
параметров, которые сами являются случайными величинами, поскольку
соответствуют случайной выборке. Оцененное (выборочное) уравнение регрессии
будет иметь вид
этих
параметров, которые сами являются случайными величинами, поскольку
соответствуют случайной выборке. Оцененное (выборочное) уравнение регрессии
будет иметь вид
![]() ,
,
где ![]() – наблюдаемые
значения ошибок
– наблюдаемые
значения ошибок ![]() .
.
Как и в случае случайных величин, параметры ![]() находятся по методу наименьших
квадратов (МНК) из условия
находятся по методу наименьших
квадратов (МНК) из условия
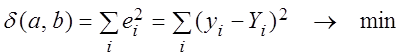 ,
,
где ![]() – значение
признака вычисленное по выборочному уравнению регрессии. Для того чтобы оценки
– значение
признака вычисленное по выборочному уравнению регрессии. Для того чтобы оценки ![]() , полученные по МНК, обладали
желательными свойствами, делаются следующие естественные предположения о
, полученные по МНК, обладали
желательными свойствами, делаются следующие естественные предположения о ![]() :
:
1)
величины ![]() являются случайными;
являются случайными;
2)
![]() ;
;
3)
дисперсии ![]() постоянны, т.е.
постоянны, т.е. ![]() ;
;
4)
значения ![]() независимы между собой, т.е.
независимы между собой, т.е. 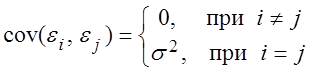 .
.
Известно, что, если условия 1 – 4
выполняются, то оценки, полученные с помощью МНК, являются несмещенными,
состоятельными и эффективными. Перечисленные свойства не зависят от конкретного
вида распределения ![]() , но обычно
предполагается, что они имеют нормальное распределение –
, но обычно
предполагается, что они имеют нормальное распределение – ![]() .
.
Найдем оценки
параметров ![]() и
и ![]() по МНК. Запишем необходимое условие
существования экстремума функции
по МНК. Запишем необходимое условие
существования экстремума функции 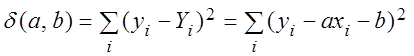 :
:
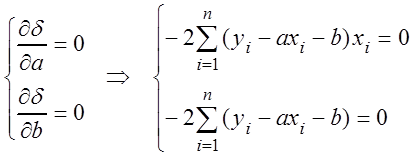 или
или 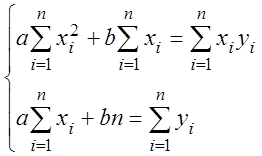 .
.
Так как 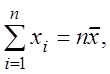
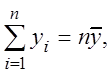
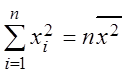 ,
,
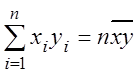 , система преобразуется к виду
, система преобразуется к виду 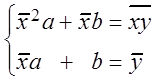 , откуда b =
, откуда b = ![]() ,
, ![]() ,
, ![]() ,
,
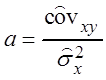 , b =
, b = 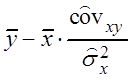 .
.
В результате выборочное уравнение линейной
регрессии ![]() на
на ![]() будет
будет
Yi = 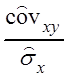 xi +
xi +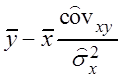 , Yi =
, Yi =![]()
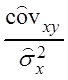 (
(![]() )
)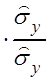 Yi =
Yi = ![]()
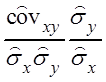 (x
(x![]() ).
).
Обозначим 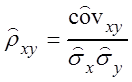 –
выборочный коэффициент корреляции, тогда окончательно получим
–
выборочный коэффициент корреляции, тогда окончательно получим
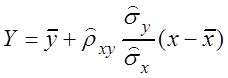 ,
,
где ![]() –
условное выборочное среднее, вычисляемое по выборочному уравнению регрессии.
–
условное выборочное среднее, вычисляемое по выборочному уравнению регрессии.
Данные наблюдений представляются в виде корреляционной таблицы.
|
x |
y1 |
y2 |
. . . |
ym |
nx |
|
x1 |
|
|
. . . |
|
|
|
x2 |
|
|
. . . |
|
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
xl |
|
|
. . . |
|
|
|
nx |
ny1 |
ny2 |
. . . |
nym |
n |
В первом столбце
указываются варианты, соответствующие первой компоненте, в первой строке –
варианты, соответствующие второй компоненте, в поле таблицы указываются ![]() – частоты появления пар
– частоты появления пар ![]() . Затем таблица дополняется еще одной
строкой
. Затем таблица дополняется еще одной
строкой ![]() и столбцом
и столбцом ![]() , где указываются
, где указываются ![]() – частота появления варианты
– частота появления варианты ![]() ,
, ![]() –
частота появления варианты
–
частота появления варианты ![]() .
.
При этом (n– объём выборки):
![]() – число различных вариант
– число различных вариант ![]() соответственно, nxi =
соответственно, nxi = 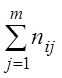 –
сумма элементов
–
сумма элементов ![]() -й строки
корреляционной таблицы, nyj =
-й строки
корреляционной таблицы, nyj = 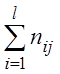 – сумма элементов
– сумма элементов ![]() -го столбца корреляционной таблицы,
-го столбца корреляционной таблицы, 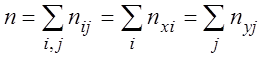 .
.
Основные выборочные характеристики вычисляются по формулам:
– выборочные средние
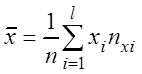 ,
, 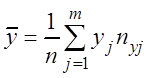 , (3.7)
, (3.7)
– выборочные дисперсии
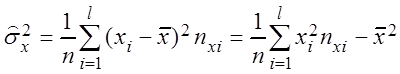 ,
, 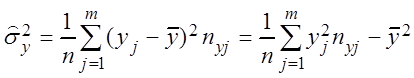 , (3.8)
, (3.8)
– выборочная ковариация
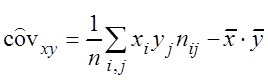 , (3.9)
, (3.9)
– выборочный коэффициент корреляции
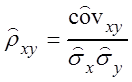 . (3.10)
. (3.10)
Если данных очень много, т.е. выборка
большого объема, то их группируют и представляют в виде двумерного
интервального распределения. Размах выборки по первой компоненте разбивается на
![]() промежутков
промежутков ![]() , а по второй – на
, а по второй – на ![]() промежутков
промежутков ![]() . Тогда интервальное статистическое
распределение представляется в виде следующей таблицы.
. Тогда интервальное статистическое
распределение представляется в виде следующей таблицы.
|
x |
[b0, b1) |
[b1, b2) |
. . . |
[bm–1, bm) |
|
|
[a0, a1) |
|
|
. . . |
|
|
|
[a1, a2) |
|
|
. . . |
|
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
[al–1, al) |
|
|
. . . |
|
|
|
|
|
|
. . . |
|
n |
Теперь в таблице: ![]() – число промежутков разбиения по
первой и второй компоненте соответственно,
– число промежутков разбиения по
первой и второй компоненте соответственно, ![]() –
число наблюдений (вариант выборки), попавших в прямоугольник со сторонами
–
число наблюдений (вариант выборки), попавших в прямоугольник со сторонами ![]() ;
; ![]() .
.
Формулы (3.7) – (3.10) для вычисления выборочных характеристик остаются в силе, но теперь: xi– середины интервалов [ai–1, ai), yj– середины интервалов [bj–1, bj).
Фактические условные средние (выборочные
средние второй компоненты, вычисленные в предположении, что первая компонента
равна ![]() ) находятся по формулам
) находятся по формулам
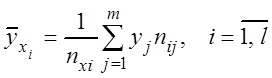 .
.
В том случае, когда варианты выборки являются равноотстоящими, т.е.
![]() ;
; ![]() ,
,
удобно числовые характеристики вычислять через условные варианты
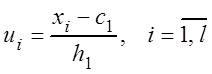 ;
;
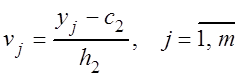 ;
;
где ![]() – условные
варианты,
– условные
варианты, ![]() – расстояния между
соседними вариантами,
– расстояния между
соседними вариантами, ![]() – ложные нули – варианты с наибольшей частотой.
– ложные нули – варианты с наибольшей частотой.
Нетрудно убедиться в том, что условные варианты
принимают только целые значения ![]() , при
этом справедливы равенства:
, при
этом справедливы равенства:
![]() ,
, ![]() ,
, ![]() ,
,
где
![]() ;
;
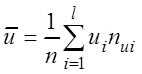 ,
, 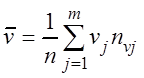 ,
,
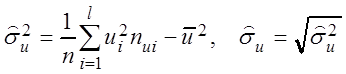 ,
, 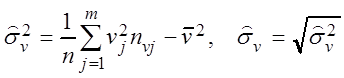 ,
,
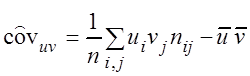 ,
, 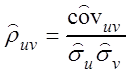 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.