Н0: Fm(x) = F0(x) – простая гипотеза,
Н0: Fm(x)Í F0 ¹ {F0(x)} – сложная гипотеза.
Гипотезы разделяются также на параметрические и непараметрические.
Параметрическиминазывают гипотезы, сформулированные относительно параметров распределения (в примере это 4 и 7), все остальные – непараметрические.
Правило, с помощью которого устанавливается справедливость или несправедливость гипотезы, называется критерием.
Если выборку рассматривать как n-мерный
вектор 
или точку вn-мерном
евклидовом пространстве Rn, то
каждый из критериев разбивает это пространство на две части, при попадании
выборки в одну из которых гипотеза Н0 принимается, а при
попадании в другую, принимается альтернативная гипотеза Н1.
Первая область – Wд называется допустимой, вторая
Wк– критической.
Rn = Wд
Wк и Wд
Wк = Æ.
Теперь, если 
Wд, то принимается гипотеза Н0, если 
Wк, то гипотеза Н0 отвергается, т.е. принимается
гипотеза альтернативная Н1.
В силу случайности выборки всегда возможны ошибки двух видов. Рассмотрим все возможные ситуации:
1) Справедлива гипотеза Н0, Wд Þ гипотеза Н0 принимается.
2) Справедлива гипотеза Н0, WкÞ
гипотеза Н0 отвергается, принимается альтернативная
гипотеза Н1.
3) Справедлива гипотеза Н1, Wд Þ принимается
гипотеза Н0.
4) Справедлива гипотеза Н1, Wк Þ гипотеза Н0 отвергается, принимается альтернативная гипотеза Н1.
1, 4 – нормальные ситуации. В ситуации 1 принимается справедливая гипотеза, в ситуации 4 отвергается несправедливая гипотеза, принимается справедливая гипо-теза .
В ситуации 2 отвергается справедливая гипотеза и это называется ошибкой первого рода.
В ситуации 3 принимается неверная гипотеза – ошибка второго рода.
Вероятность ошибки первого рода – aназывается уровнем значимости критерия, т.е. по определению
.
Вероятность ошибки второго рода – 
называется оперативной
характеристикой критерия. Здесь по определению
.
В статистике предпочитают иметь дело с мощностью критерия – b:
.
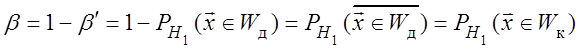Желание любого исследователя получить такой критерий, при котором вероятности ошибок первого и второго рода были минимальны, в идеале – их не было вообще. Но это невозможно, так как уменьшение вероятности ошибки первого рода приводит к расширению допустимой области (сужению Wк) и, как следствие, к увеличению вероятности ошибки второго рода, а уменьшение вероятности ошибки второго рода приводит к расширению критической области (сужению Wд) и увеличению вероятности ошибки первого рода. В связи с этим, на практике поступают следующим образом: гипотеза проверяется по возможности большим числом критериев и среди них выбирается тот, мощность которого наибольшая. Уровень значимости при a, как правило, выбирается из ряда 0,001; 0,005; 0,01; 0,05; 0,1
Если уровень значимости критерия известен
и равен a, то по случайной выборке 
строится некоторая функция r = r(),
характеризующая меру отклонения теоретической функции распределения от эмпирической.
При этом допустимая область определяется из условия:
Р(r > с) = a.
В случае справедливости гипотезы 
, данное равенство будет равносильно
следующему:
a = Р(r > с) = 1 – Fr(c), или 
= 1 – a,
отсюда 
, т.е. с –
квантиль уровня (1 – a), и значит
допустимая область определяется неравенством
Величина с называется критическим значением
критерия, будем обозначать ее 
.
Для проверки гипотезы по выборке
вычисляется наблюдаемое значение критерия 
и,
если 
, – принимается гипотеза Н0,
если 
, – принимается гипотеза Н1,
соответственно гипотеза Н0 отвергается (рис. 3.1).
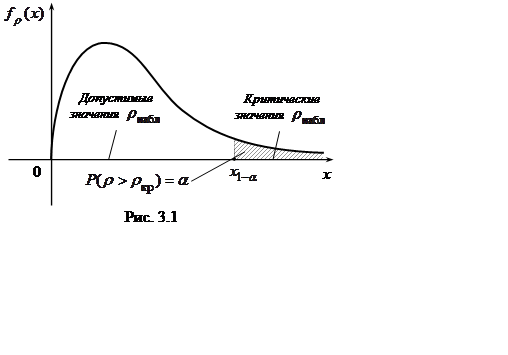Обычно уровень значимости выбирается
настолько малым, чтобы событие, вероятность которого равна a, можно было считать практически невозможным.
Если ,
то это событие происходит (происходит событие, которое считается практически
невозможным), значит в этом случае гипотеза Н0
скорее всего несправедлива. В противном случае, когда ,гипотеза Н0 возможно может быть принята.
3.4.2. Простые гипотезы
Предположим, что по выборке сформулированы две простые гипотезы:
H0: Fm(x) = F0(x), H1: Fm(x) = F1(x).
В этом случае, оказывается, существует наиболее мощный критерий, который называется критерием отношения правдоподобия, и имеет следующий вид:
,
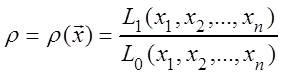где в числителе - функция правдоподобия, вычисленная в предположении справедливости гипотезы Н1, а в знаменателе – Н0.
Если справедлива гипотеза Н0, то это отношение меньше единицы, если справедлива гипотеза Н1, это отношение больше единицы. Критическое отношение определяется по уровню значимости.
Теорема 3.3 (Неймана-Пирсона)
Из всех критериев, проверяющих простые гипотезы, критерий отношения правдоподобия является наиболее мощным.
3.4.3. Критерии согласия
Имеется случайная выборка 
. Необходимо проверить гипотезу H0: Fm(x) = F0(x),
при альтернативной гипотезе H1: Fm(x) ¹ F0(x).
Здесь основная гипотеза является простой, и, в случае ее справедливости мы получаем полную информацию о распределении количественного признака генеральной совокупности. Альтернативная гипотеза - сложная и в случае ее справедливости не дает вообще никакой информации о генеральной совокупности.
Поэтому критерии, проверяющие гипотезу H0 при альтернативной гипотезе H1, называются критериями согласия, так как здесь мы отвечаем на вопрос, согласуются ли результаты наблюдений с выдвинутой гипотезой H0.
Критерий Колмогорова
Здесь критерий строится на основе статистики вида
.
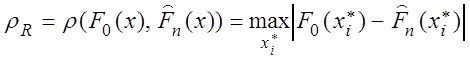Независимо от предполагаемой функции распределения F0(x) при n ® ¥величина 
стремится
к закону распределения Колмогорова К(х), поэтому
P(r > с) = a, 1 – P(r < с) = a, 1 – K(c) = a, K(c) = 1 – a,
c
= 
(1
– a) = x1-a
– квантиль уровня (1 – a) для распределения
Колмогорова.
Критерий Колмогорова предписывает принять гипотезу 
, если
,
и отвергнуть ее в противном случае.
Критерий c2 (Пирсона)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.