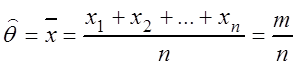Математика \ Теория вероятностей и математическая статистика

Математическая статистика (Основные задачи и понятия математической статистики. Точечные оценки параметров распределения. Основные методы получения точечных оценок. Проверка статистических гипотез. Линейная регрессия), страница 2

В качестве оценки параметра q рассмотрим относительную частоту появления события А в этих испытаниях, т.е.

,

где m – число появления события А в n испытаниях. Случайная величина m распределена по биномиальному закону, следовательно,искомое распределение будет иметь следующий вид:

P( = k) =  .

0

. . .

. . .

1

P

. . .

. . .

Так как  – случайная величина и выборка тоже многомерная случайная величина в математической статистике, как правило, мы не гарантированы от сколь угодно больших ошибок. Значит, гарантировать достаточную близость оценки  к оцениваемому параметру можно лишь с некоторой вероятностью и, для того чтобы увеличить эту вероятность, приходится увеличивать объем выборки.

Главное свойство любой оценки, оправдывающее само название "оценка" – возможность, хотя бы ценой увеличения объема выборки до бесконечности, получить точное значение неизвестного параметра

Поэтому оценка  называется состоятельной, если с ростом объема выборки она сходится к оцениваемому параметру, т.е. при всех возможных значениях параметра :

.

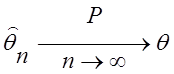Выборочной средней –  называется среднее арифметическое вариант выборки

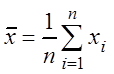
Выборочной дисперсией –  называется среднее арифметическое квадратов отклонения вариант от выборочной средней

,

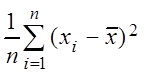Для любой случайной величины :  – точечная оценка для математического ожидания М(m),  – точечная оценка для дисперсии D(m).

Получим полезную для дальнейшего изложения формулу, так как  

,

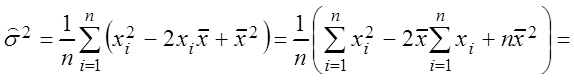
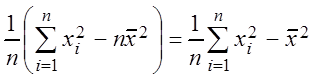то

,

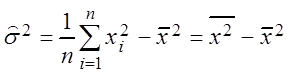С помощью аналогичных выкладок можно показать справедливость равенства

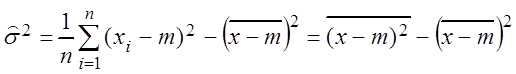,                  (3.1)

где  m = M(m).

Покажем состоятельность этих оценок:

1)   .

По теореме Чебышева

 

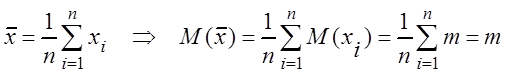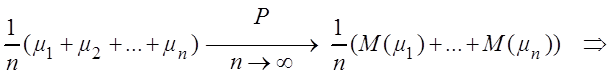
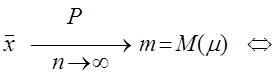
 – состоятельная оценка для М(m).

2) .

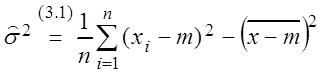По теореме Чебышева, рассматривая случайные величины mi = (xi – m)2, получаем:

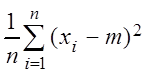
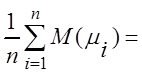
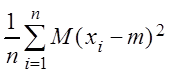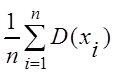
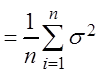  == D(m).

второе слагаемое  0  D(m)

– это и означает состоятельность оценки.

Величина d(,q) = М() – q  называется смещением оценки  относительно параметра q.

Оценка  называется несмещённой, если d(,q) = 0  Û  М() = q .

Несмещённость выборочной средней : 

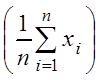
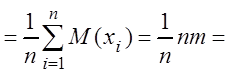М() = М m = M(m) = q   

оценка  является несмещенной для M(m).

Смещенность выборочной дисперсии :

M()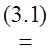M.     (*)

Здесь использовано равенство

= =.

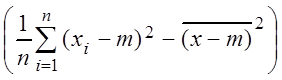
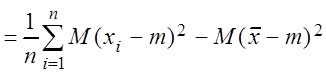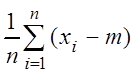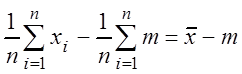Рассматриваем первое слагаемое в равенстве (*). Здесь xi– одинаково распределенные независимые случайные величины, следовательно,

M(xi– m)2=D(xi)=D(m),  =.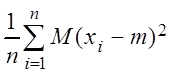

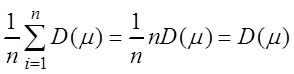Второе слагаемое в равенстве (*):

 = D() = D=.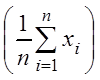

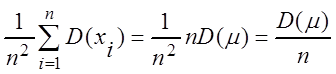Таким образом,

= D(m) – D(m) =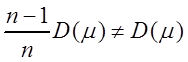     

 – смещённая оценка для дисперсии .

Исправленная выборочная дисперсия  – это величина, равная

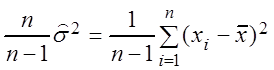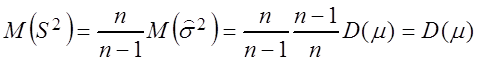 =    Þ     Þ

 – несмещённая оценка для дисперсии случайной величины.

На практике используется и , и , так как   .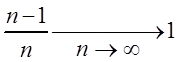

Очевидно, что для любого параметра можно рассматривать бесконечное множество оценок и из всех этих оценок желательно выбрать ту, которая имеет наименьший разброс. Мерой разброса случайной величины является дисперсия

.

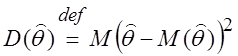Но для смещённых оценок мы получаем меру отклонения не от оцениваемого параметра, а от математического ожидания . Поэтому следующее требование предъявляется к несмещённым оценкам, тогда и .

Оценка  называется эффективной, если при любом значении параметра q дисперсия этой оценки минимальна, т.е.  выбирается из условия:

.

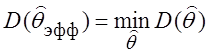Теорема 3.2. Для произвольной оценки  параметра распределения q  выполняется неравенство:

,

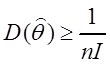где  – информация Фишера.

Информация Фишера для дискретной случайной величины вычисляется по формуле

, .

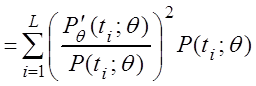            Здесь, если закон распределения случайной величины  имеет вид

m

t1

t2

. . .

tL

P

p1

p2

. . .

pL

то закон распределения случайной величиныh = Р(m; q) будет следующим

p1

p2

. . .

pL

P

p1

p2

. . .

pL

Для непрерывной случайной величины информация Фишера вычисляется по формуле

.

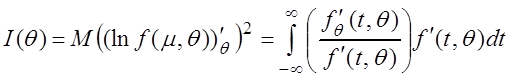Величина 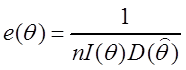 называется эффективностьюоценки.

Очевидно, что 0 < e(q) £1, причём, если e(q) = 1,то дисперсия оценки  будет минимальной, т.е. по определению эта оценка будет эффективной.

Оценка  называется эффективной по Рао-Крамеру, если ее эффективность равна единице, т.е. e(q) = 1. Рассмотрим несколько примеров.

Пример 3.2. В схеме n последовательных испытаний Бернулли q = p = P(A), mi – число появлений события А в i-м испытании. Закон распределения mi

mi

0

1
P

1–q

q

Пусть 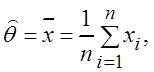 доказать, что эта оценка является эффективной.

Решение. Закон распределения случайной величины h = P(m, q) имеет вид

h

1–q

q
P

1–q

q

тогда P(0; q) = 1 – q,  P(1; q) = q,

,

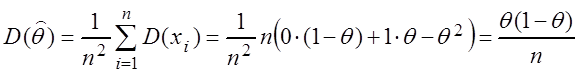I(q) =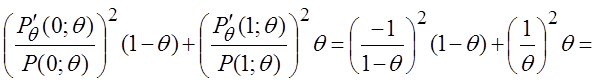

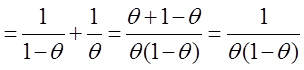   Þ   ,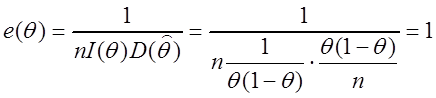

следовательно, данная оценка является эффективной для вероятностиp = P(A).

Пример 3.3. Рассмотрим нормальный закон распределения с параметрами m, s2, в котором дисперсия s2 известна, а неизвестен параметр . Пусть . Установить, является ли эта оценка эффективной.

            Решение. Здесь

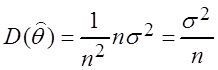,  f(m; q) = ,

,

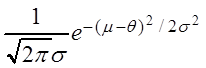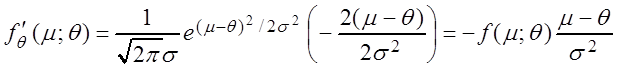I(q) ,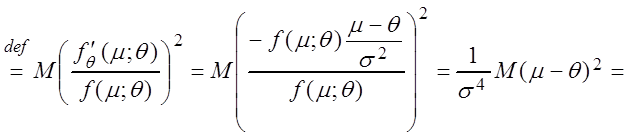

,

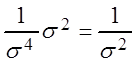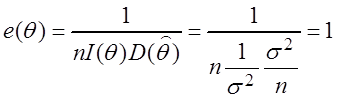следовательно, данная оценка является эффективной.

Пример 3.4. В показательном распределении

неизвестен параметр . Убедиться, что  – эффективная оценка для этого параметра.

Решение. Из курса теории вероятностей известно, что для показательного распределения

М(m) = ,    D(m) = .

Пусть q =  = М(m) тогда 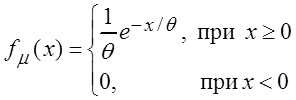  и  является точечной оценкой для параметра

   

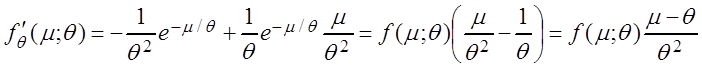
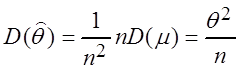, I(q) = ,

,

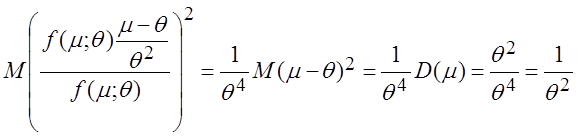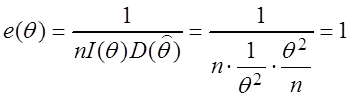значит оценка  является эффективной для 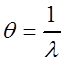, следовательно  – эффективная оценка для .

3.3. Основные методы получения точечных оценок

3.3.1. Метод моментов

По аналогии с определением начальных и центральных моментов k-го порядка случайной величины, по данным случайной выборки можно определить начальные и центральные выборочные моменты k-го порядка.

Скачать файл