Математическая статистика (Основные задачи и понятия математической статистики. Точечные оценки параметров распределения. Основные методы получения точечных оценок. Проверка статистических гипотез. Линейная регрессия), страница 3

Начальным выборочным моментом k-го порядка  называется среднее арифметическое k-х степеней вариант выборки, т.е.

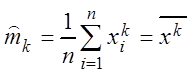
Центральным выборочным моментом k-го порядка  называется среднее арифметическое k-х степеней отклонения вариант выборки от выборочного среднего, т.е.

.

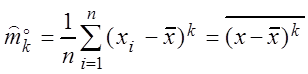Эти выборочные моменты являются точечными оценками соответствующих теоретических моментов случайной величины m.

Если  F_m(x) = F(x; q₁, q₂, ... , q_r)  зависит от r параметров,  то естественно потребовать, чтобы моменты k-го порядка случайной величины mсовпадали с выборочными моментами этого же порядка, т.е.

m_k = ,  k =     или    =     k = .

В частности, если  m – непрерывная случайная  величина и f_m(x) = f(x; q) , то

,

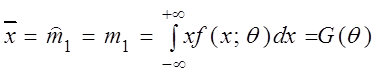отсюда формально находим .

Пример 3.5. По данным случайной выборки найти точечную оценку для параметра l показательного распределения.

.

Решение.q = l,  ,   .

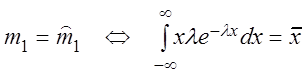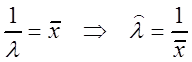Пример 3.6. Найти точечные оценки для границ a и bравномерного распределения на отрезке [a, b].

Решение. Записываем равенства теоретических и выборочных начальных моментов двух первых порядков

.

, 

,

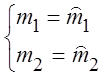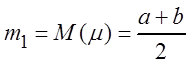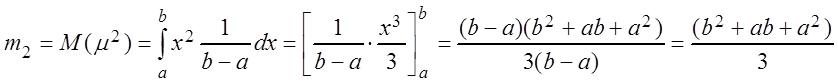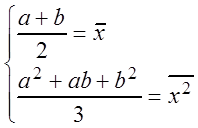 ,        b = 2 – a,    a² + 2a – a² + (2 – a)² = 3,

a² + 2a – a² + 4 – 4a + a² = 3,   a² – 2a + 4 – 3= 0,

,

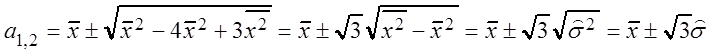b_1,2 = 2 – () = ,

так как по определению плотности равномерного распределения a < b, получаем

;        = .

3.3.2. Метод наибольшего правдоподобия

Пусть  – дискретная случайная величина, заданная законом распределения:

Рассмотрим функцию вида L = L(x₁, x₂, _{. . .} x_n; q) = P(x₁; q)P(x₂; q)×...×P(x_n; q), которая называется функцией правдоподобия. Здесь P(x_i; q) = P(m = x_i).

Функция правдоподобия представляет собой вероятность получения (реализации) выборки. А так как выборка уже имеется, т.е. реализована, то значение этой функции должно быть равно 1. Но в силу случайного характера, как  правило, эта функция отлична от 1, но должна быть, по крайней мере, максимальной. Записав необходимое условие существования экстремума (max), получаем уравнение:

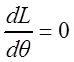                    ,                                                          (3.2)

которое называется уравнением правдоподобия.

Решение этого уравнения –  называется оценкой наибольшего правдоподобия.

Если закон распределения зависит не от одного, а от r параметров, рассуждая аналогично, получим систему уравнений (необходимое условие существования экстремума функции нескольких переменных).

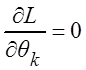                                          ,   k=.                                                  (3.3)

            Функция L является произведением nфункций, а n , как правило, очень велико. Поэтому левые части уравнений (3.2) и (3.3), как правило, будут вычисляться очень сложно. Поэтому часто рассматривается логарифмическая функция правдоподобия

= lnL=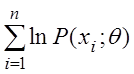

теперь это уже сумма  слагаемых, производная которой вычисляется значительно проще.

В силу монотонности логарифмической функции, точки экстремума функцийLи   будут совпадать. Поэтому (3.2) 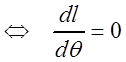; а  (3.4) 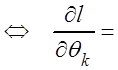 0 ,  k = .

Пример 3.7. По имеющейся случайной выборке , x_i Î N{0} найти оценку наибольшего правдоподобия для параметра l случайной величины m, распределённой по закону Пуассона: .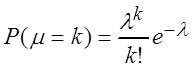

Решение. Строим функцию правдоподобия:

;         .

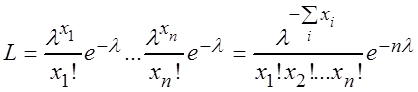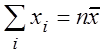Обозначим 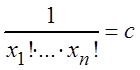, тогда

L = c,    ,

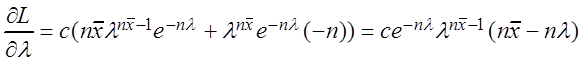(3.3)    , отсюда   .

Если  - непрерывная случайная величина, то в этом случае функция правдоподобия определяется из равенства:

L(x₁, ..., x_n; q)D x₁ . . . D x_n = f(x₁; q)Dx_{1 . . .} f(x_n; q)Dx_n ,

в правой части которого вероятность того, что многомерная случайная величина   = (x₁, ..., x_n) примет значение из параллелепипеда со сторонами: Dx₁, Dx₂, ..., Dx_n. Из этого равенства находим L = f(x₁; q) _... f(x_n; q) , т.е. функция правдоподобия пропорциональна вероятности реализации выборки, значит и для непрерывной случайной величины справедливы ранее записанные уравнения (3.2), (3.3).

Пример 3.8. Найти оценки наибольшего правдоподобия m, s нормального распределения.

Решение. Пусть q₁ = m,  q₂ = s,  .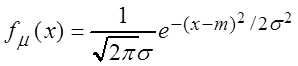

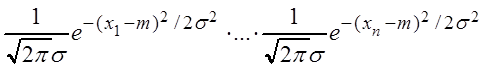
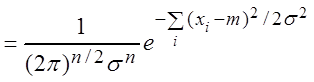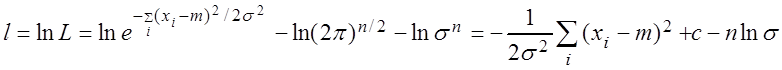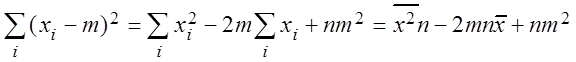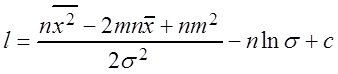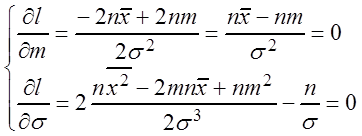Функция правдоподобия имеет вид

,

,

.

Таким образом,

, 

,   m = ,   ,

,  .

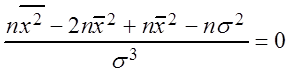Таким образом,  ,  .

Оценки наибольшего правдоподобия всегда являются состоятельными и эффективными.

3.4. Проверка статистических гипотез

3.4.1. Основные понятия

Любое предположение, основанное на результатах анализа случайной выборки  относительно теоретической функции распределения, называется статистической гипотезой (или гипотезой).

Например, в схеме Бернулли:

1)  вероятность появления события А в отдельном испытании равна 0,4,

2)  вероятность появления события А в отдельном испытании р> 0,7,

3)  вероятность появления события А в отдельном испытании 0,3 < p < 0,4

или в общем случае;

4)  случайная величина m распределена по нормальному закону с параметрами: m = 0,  s = 1,

5)  при нормальном законе распределения D(m) = s²£ M²(m),

6)  случайная величина m распределена по показательному закону,

7)  случайная величина распределена по показательному закону, параметр которого 1£ l£ 2.

Основная задача – по результатам случайной выборки определить: справедлива или несправедлива выдвинутая гипотеза.

С любой гипотезой можно рассматривать непересекающуюся гипотезу. Одна из них называется основной гипотезой – H₀, вторая – конкурирующей или альтернативной – H₁.

Это разделение условно. Обычно в качестве основной гипотезы принимается та, которая несёт больше информации о теоретической функции распределения.

Все гипотезы разделяются на простые и сложные.

Гипотезаназывается простой, если она полностью определяет теоретическую функцию распределения (в примере это гипотезы 1 и 4), все остальные гипотезы называются сложными.

Каждая из гипотез выделяет некоторый класс функций распределения.

Обозначим эти множества: F₀ и F₁, тогда: