Гетерогенные каталитические реакторы. Влияние диффузии внутри пор на селективность. Дезактивация катализатора, страница 7

В случае быстрых каталитических реакций может иметь случай, когда скорость реакции лимитируется внешней диффузией вещества к грануле. Обозначив концентрацию вне гранулы С_1b, концентрацию на внешней поверхности гранулы С_1S, баланс массы для вещества А₁ на единицу реакционного объема, можно записать в виде (для стационарных условий):

                                             (1.63)

где - скорость реакции на внешней поверхности гранулы (С₁=С_1S) в моль/ (с×кг)

Для реакции 1^го порядка

                                                                 (1.64)

Из (1.63) и (1.64) можно получить:

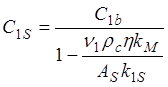                                                             (1.65)

Если суммарный коэффициент массопереноса К₁, определяется из:

                                                               (1.66)

можно получить

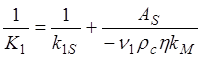                                                       (1.67)

К₁ – это суммарный коэффициент массопереноса, учитывающий внешний массоперенос (k_1S), диффузию в порах (h), и химическую реакцию (k_M).

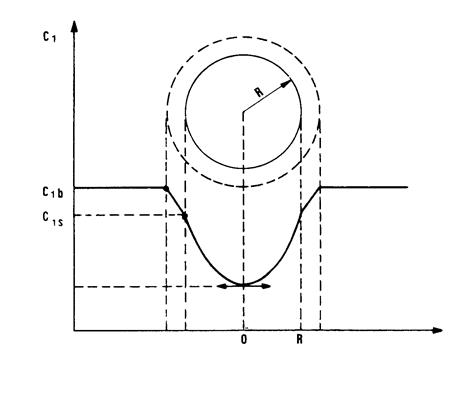
На рис. 1.5 показан типичный концентрационный профиль вокруг и внутри активной частицы катализатора.

Некоторые предельные случаи.

Случай 1

Катализатор состоит из сферических гранул диаметром d_p:

                                                     (1.68)

В этом случае:

                                                   (1.69)

Случай 2

Катализатор состоит из таблеток H=D:

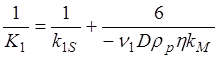                                                    (1.70)

Рис. 1.5 Концентрационный профиль вокруг и внутри активной части катализатора

1.8.2. Концепция суммарной эффективности гранулы

Так же, как и в случае определения эффективности гранулы при наличии внутренней диффузии можно определить суммарную эффективность e. А именно, определим e как отношение потока реактанта на единицу объема реактора к теоретическому потоку, определенному в предположении, что концентрация и температура и концентрация в газовой (жидкой) фазе равны Т_b и С_1b, соответственно. Для реакции первого порядка:

                                         (1.71)

откуда

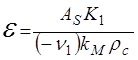                                                         (1.72)

Можно показать, что

                                                         (1.73)

В дополнение к числам Пратера, Тиле и Аррениуса (Ф, b₁, b₂) суммарная эффективность зависит еще от двух безразмерных величин теплового и массообменного чисел Био:

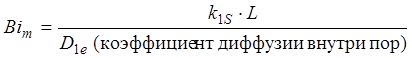                            (1.74)

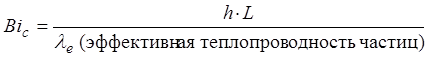                         (1.75)

где L – характерный размер, h – коэффициент теплопереноса в газообразную (жидкую) фазу.

Карберри детально исследовал данный вопрос теоретически. Анализируя величину e в зависимости от упомянутых безразмерных величин (1.74), (1.75), можно обнаружить множественность стационарных состояний, связанных с внутренними градиентами (об этом уже говорилось) и внешними градиентами или с совместным существованием внутренних и внешних градиентов. Тем не менее, такие случаи редко встречаются на практике.

1.9. Температурные и концентрационные градиенты

Для гетерогенных каталитических реакций с участием газовой фазы, можно получить:

(а)Внутренние температурные градиенты обычно малы (редко > нескольких градусов  между Т_S и внутренней температурой гранулы.)

(б)Внешний градиент температур может быть высоким (разница температур Т_S – Т_b может составлять несколько десятков градусов.)

(в)Внутренний концентрационный градиент может быть высоким (иногда внутри зерна концентрация может быть равна 0).

(г)Внешний концентрационный градиент обычно мал, исключая случай очень быстрых реакций.

Для гетерогенных реакций с участием жидкой фазы, можно установить, что:

(а)Внутренний температурный градиент мал.

(б)Внешний температурный градиент мал.

(в)Внутренний концентрационный градиент существенно зависит от активности катализатора.