Гетерогенные каталитические реакторы. Влияние диффузии внутри пор на селективность. Дезактивация катализатора, страница 2

Суммарная скорость реакции в порах катализатора может зависеть от процесса диффузии исходных реагентов и продуктов реакции в порах. Фактически, увеличение скорости изменения содержания реагирующих веществ в реакторе не должно происходить пропорционально увеличению удельной поверхности гранул. По этой причине проблема приготовления катализаторов оптимальной текстуры должна решаться на основе рассмотрения транспорта реактантов и продуктов реакции в порах.

Рассмотрим эту проблему в идеальном случае каталитической реакции, протекающей в сферическом пористом зерне гомогенной структуры, то есть с активными местами равномерно распределенными по объему зерна. На рис. 1.1 изображена гранула радиусом R и типичный профиль концентрации реагирующего вещества внутри нее. Выделим сферический слой dz, и рассмотрим баланс массы для этого слоя.

Пусть гранула радиусом R погружена в газообразную или жидкую среду, содержащую реактант А₁, который в контакте с катализатором участвует в реакции

n₁A₁+n₂A₂=0, r'=k_MC₁

Это реакция первого порядка, где r' выражается в моль/сек (кг катализатора) (в этих условиях, константа скорости реакции k_m выражается в m³/с (кг катализатора)). Вводя эффективный коэффициент диффузии D_e, мы можем использовать выражение подобное закону Фика, чтобы записать уравнение баланса для сферического слоя толщиной dz в результате реакции и расход вещества через сферическую поверхность радиусом z+dz.

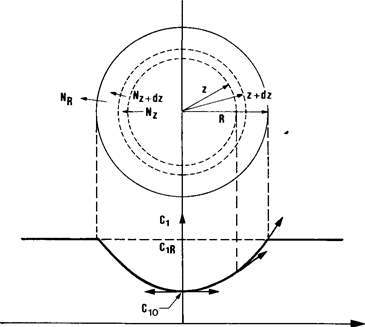
Рис. 1.1 Диффузионные потоки в сферическом слое гранулы катализатора и типичный концентрационный профиль в грануле.

В соответствии с рис.1.1 поток вещества через поверхность радиуса z в единицу времени:

                                                               (1.12)

Количество вещества, образующегося (исчезающего) в единицу времени внутри слоя: 

                                                                   (1.13)

поток вещества через поверхность радиуса z+dz в единицу времени

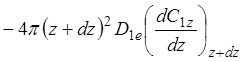                                                      (1.14)

Складывая, преобразуя и упрощая, баланс можно записать в виде:

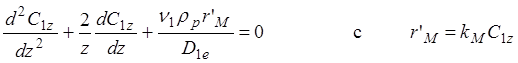                  (1.15)

Это дифференциальное уравнение может быть решено с использованием следующих граничных условий

                                                        (1.16)

(из условий симметрии)               (1.17)

где С_1R – концентрация вещества А₁ на внешней поверхности гранулы.

Делая замену переменой y=zC_1z, можно записать:

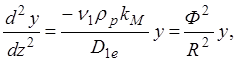                                                   (1.18)

где

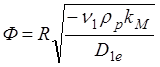                                                            (1.19)

Общее решение (1.18) можно получить в виде:

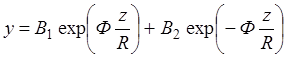                                                  (1.20)

Граничные условия перепишутся в виде:

для    z = 0                         y = 0                следовательно  В₁ = - В₂

для     z = R                        y = RC_1R                                                              (1.21)

При этом имеем:

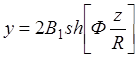                                                           (1.22)

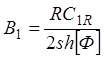                                                                 (1.23)

Ф, определяемая (1.19) – безразмерное число, называемое модулем Тиле. Его можно записать также в виде:

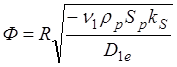                                                      (1.24)

Окончательно решение (1.15):

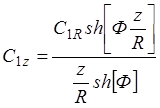                                                        (1.25)

Разлагая sh [z/R] в ряд в окрестности точки z = 0, получим:

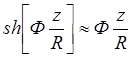                                                           (1.26)

Подставляя (1.26) в (1.25), можно получить

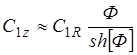                                                          (1.27)

Дифференцируя (1.25) получим:

                                      (1.28)

Это выражение всегда >0.

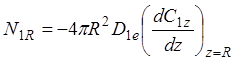                                             (1.29)

Подставляя в (1.29) dC_1z/dz при z = R из (1.28) ®

                                      (1.30)

или

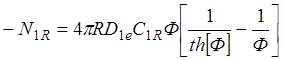                                          (1.31)

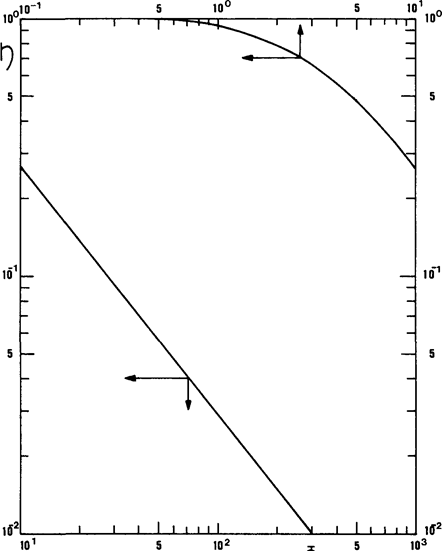
Рис. 1.2 Соотношение между эффективностью и модулем Тиле.